Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 sở GDĐT Bắc Giang

Câu 1  (3 điểm):

1) Làm tính nhân : $2x.\left( {5{x^2} - x + \dfrac{1}{2}} \right) \cdot$

2) Tính nhanh ${2020^2} - {2019^2}.$

3) Phân tích các đa thức sau thành  nhân tử :

a) $8{x^2} - 18{x^3}.$

b) ${x^3} - 3{x^2} - 4x + 12.$

Câu 2 (2 điểm):

1) Tìm $x$ biết $2\left( {x + 3} \right) - 6x\left( {x + 3} \right) = 0.$

2) Thực hiện phép tính $\left( {{x^4} - 3x - {x^3} - 3{x^2} - 18} \right):\left( {{x^2} + 3} \right)$

Câu 3 (1,5 điểm): Cho biểu thức $C = \dfrac{4}{{x + 2}} + \dfrac{3}{{2 - x}} + \dfrac{{12}}{{{x^2} - 4}},$ với $x \ne 2$ và $x \ne 2.$

1) Rút gọn biểu thức $C.$

2) Tìm các giá trị của $x$ để $C =  - \dfrac{1}{2} \cdot$

Câu 4 (3 điểm):

Cho tam giác $ABC$ vuông tại $A,$ có đường trung tuyến $AM.$ Gọi $D$ là trung điểm của $AB,$ $E$ là điểm đối  xứng với điểm $M$ qua $D.$

1) Chứng minh tứ giác $AEBM$ là hình bình hành.

2) Chứng minh điểm $E$ đối xứng với điểm $M$ qua $AB.$

3) Tam giác vuông $ABC$ có điều kiện gì thì tứ giác $AEBM$ là hình vuông ?

Câu 5 (0,5 điểm):

Tìm đa thức $f\left( x \right)$ biết rằng : $f\left( x \right)$ chia cho $\left( {x + 2} \right)$ dư $10,$ $f\left( x \right)$ chia cho $\left( {x - 2} \right)$ dư $24,$ $f\left( x \right)$ chia cho $\left( {{x^2} - 4} \right)$ được thương là $- 5x$ và còn dư.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

Câu 1 (VD):

Phương pháp:

1) Nhân đơn thức với đa thức $A\left( {B + C} \right) = AB + AC$

2) Sử dụng hằng đẳng thức ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$

3) Dùng phương pháp đặt nhân tử chung, hằng đẳng thức và nhóm hạng tử thích hợp để phân tích

Cách giải:

1) Làm tính nhân : $2x.\left( {5{x^2} - x + \dfrac{1}{2}} \right) \cdot$

Ta có:

$\begin{array}{l}2x.\left( {5{x^2} - x + \dfrac{1}{2}} \right) = 2x.5{x^2} - 2x.x + 2x.\dfrac{1}{2}\\ = 10{x^3} - 2{x^2} + x\end{array}$

2) Tính nhanh ${2020^2} - {2019^2}.$

Ta có:

$\begin{array}{l}{2020^2} - {2019^2} = \left( {2020 - 2019} \right)\left( {2020 + 2019} \right)\\ = 1.4039 = 4039\end{array}$

3) Phân tích các đa thức sau thành  nhân tử :

a) $8{x^2} - 18{x^3} = 2{x^2}\left( {4 - 9{x^2}} \right)$$= 2{x^2}\left( {2 - 3x} \right)\left( {2 + 3x} \right)$

b) ${x^3} - 3{x^2} - 4x + 12 = {x^2}\left( {x - 3} \right) - 4\left( {x - 3} \right)$$= \left( {x - 3} \right)\left( {{x^2} - 4} \right) = \left( {x - 3} \right)\left( {x - 2} \right)\left( {x + 2} \right)$

Câu 2 (VD):

Phương pháp:

1) Phân tích vế trái thành nhân tử để đưa về dạng $A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.$

2) Phân tích thành nhân tử rồi chia hoặc thực hiện phép chia dọc

Cách giải:

1) Tìm $x$ biết $2\left( {x + 3} \right) - 6x\left( {x + 3} \right) = 0.$

Ta có: $2\left( {x + 3} \right) - 6x\left( {x + 3} \right) = 0$

$\begin{array}{l} \Leftrightarrow \left( {2 - 6x} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2 - 6x = 0\\x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{3}\\x =  - 3\end{array} \right.\end{array}$

Vậy $x = \dfrac{1}{3};x =  - 3.$

2) Thực hiện phép tính $\left( {{x^4} - 3x - {x^3} - 3{x^2} - 18} \right):\left( {{x^2} + 3} \right)$

Ta có:

$\begin{array}{l}\left( {{x^4} - 3x - {x^3} - 3{x^2} - 18} \right):\left( {{x^2} + 3} \right)\\ = \left( {{x^4} - {x^3} - 3{x^2} - 3x - 18} \right):\left( {{x^2} + 3} \right)\end{array}$

$= \left( {{x^4} + 3{x^2} - {x^3} - 3x - 6{x^2} - 18} \right):\left( {{x^2} + 3} \right)$

$= \left[ {{x^2}\left( {{x^2} + 3} \right) - x\left( {{x^2} + 3} \right) - 6\left( {{x^2} + 3} \right)} \right]:\left( {{x^2} + 3} \right)$

$\begin{array}{l} = \left( {{x^2} - x - 6} \right)\left( {{x^2} + 3} \right):\left( {{x^2} + 3} \right)\\ = {x^2} - x - 6\end{array}$

Câu 3 (VD):

Phương pháp:

1) Qui đồng mẫu các phân thức rồi cộng trừ và rút gọn

2) Biến đổi đưa về dạng tìm $x$ thường gặp

Cách giải:

Cho biểu thức $C = \dfrac{4}{{x + 2}} + \dfrac{3}{{2 - x}} + \dfrac{{12}}{{{x^2} - 4}},$ với $x \ne 2$ và $x \ne 2.$

1) Rút gọn biểu thức $C.$

Ta có:

$\begin{array}{l}C = \dfrac{4}{{x + 2}} + \dfrac{3}{{2 - x}} + \dfrac{{12}}{{{x^2} - 4}}\\ = \dfrac{{4\left( {x - 2} \right) - 3\left( {x + 2} \right) + 12}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \dfrac{{4x - 8 - 3x - 6 + 12}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \dfrac{{x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \dfrac{1}{{x + 2}}\end{array}$

Vậy $C = \dfrac{1}{{x + 2}}\,\,\left( {x \ne 2;x \ne  - 2} \right)$

2) Tìm các giá trị của $x$ để $C =  - \dfrac{1}{2} \cdot$

Để $C =  - \dfrac{1}{2}$

$\begin{array}{l} \Leftrightarrow \dfrac{1}{{x + 2}} =  - \dfrac{1}{2}\,\,\,\,\left( {x \ne 2;x \ne  - 2} \right)\\ \Rightarrow x + 2 =  - 2\\ \Leftrightarrow x =  - 4\left( {tm} \right)\end{array}$

Vậy với $x =  - 4$ thì $C =  - \dfrac{1}{2}.$

Câu 4 (VD):

Phương pháp:

1) Sử dụng dấu hiệu nhận biết: Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành

2) Sử dụng tính chất đường trung bình và kiến thức về đối xứng trục

3) Hình bình hành có hai đường chéo vuông góc là hình thoi

Hình thoi có 1 góc vuông là hình vuông

Cách giải:

Cho tam giác $ABC$ vuông tại $A,$ có đường trung tuyến $AM.$ Gọi $D$ là trung điểm của $AB,$ $E$ là điểm đối  xứng với điểm $M$ qua $D.$

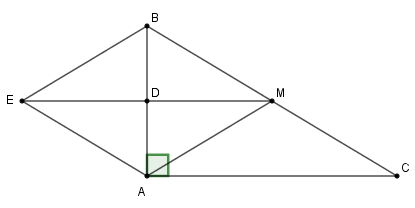
1) Chứng minh tứ giác $AEBM$ là hình bình hành.

Xét tứ giác $AEBM$ có $D$ là trung điểm của AB và D là trung điểm EM (do E đối xứng với M qua D) nên hai đường chéo AB và EM giao nhau tại trung điểm mỗi đường

Suy ra AEBM là hình bình hành (dấu hiệu nhận biết)

2) Chứng minh điểm $E$ đối xứng với điểm $M$ qua $AB.$

Ta có D là trung điểm cạnh AB và M là trung điểm cạnh BC nên DM là đường trung bình của tam giác ABC

Hay $DM//AC \Rightarrow EM//AC$

Mà $AB \bot AC \Rightarrow AB \bot EM$ tại D.

Mà D là trung điểm EM nên AB là đường trung trực của đoạn EM.

Hay E đối xứng với M qua AB.

3) Tam giác vuông $ABC$ có điều kiện gì thì tứ giác $AEBM$ là hình vuông ?

Xét hình bình hành AEBM có hai đường chéo AB và EM vuông góc với nhau nên AEBM là hình thoi

Để hình thoi AEBM là hình bình hành thì $\widehat {AMB} = {90^0}$ hay $AM \bot BC$

Mà AM là đường trung tuyến của tam giác ABC nên tam giác ABC có AM vừa là đường trung tuyến và vừa là đường cao.

Suy ra tam giác ABC cân tại A.

Vậy tam giác ABC vuông cân tại A thì AEBM là hình vuông.

Câu 5 (VDC):

Phương pháp:

Từ điều kiện đề bài viết được dạng tổng quát của đa thức $f\left( x \right)$

Từ đó tính $f\left( { - 2} \right) = 10;f\left( 2 \right) = 24$ để suy ra $f\left( x \right)$

Cách giải:

Vì $f\left( x \right)$ chia cho $\left( {{x^2} - 4} \right)$ được thương là $- 5x$ và còn dư nên phần dư có dạng $ax + b.$

Suy ra $f\left( x \right) = \left( {{x^2} - 4} \right).\left( { - 5x} \right) + ax + b$

Vì $f\left( x \right)$ chia cho $\left( {x + 2} \right)$ dư $10$ nên $f\left( { - 2} \right) = 10$

Ta có $f\left( { - 2} \right) = 10$ $\Leftrightarrow a.\left( { - 2} \right) + b =  - 10 \Rightarrow b =  - 10 + 2a$ (1)

Vì $f\left( x \right)$ chia cho $\left( {x - 2} \right)$ dư $24$ nên $f\left( 2 \right) = 24$

Ta có: $f\left( 2 \right) = 24 \Rightarrow 2a + b = 24$ $\Rightarrow b = 24 - 2a$ (2)

Từ (1) và (2) suy ra $2a - 10 = 24 - 2a \Rightarrow 4a = 34$ $\Leftrightarrow a = \dfrac{{17}}{2}$

Suy ra $b = 2a - 10 = 2.\dfrac{{17}}{2} - 10 = 7$

Nên $f\left( x \right) = \left( {{x^2} - 4} \right).\left( { - 5x} \right) + \dfrac{{17}}{2}x + 7$

Hay $f\left( x \right) =  - 5{x^3} + \dfrac{{57}}{2}x + 7$

HẾT

Loigiaihay.com