Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 10. Diện tích hình tròn, hình quạt tròn

Đề kiểm tra 15 phút - Đề số 4 - Bài 10 - Chương 3 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 10 - Chương 3 - Hình học 9

Đề bài

Cho ∆ABC đều cạnh A, trên nửa mặt phẳng bờ BC chứa điểm A, vẽ nửa đường tròn đường kính BC. Hãy tính diện tích phần hình tròn nằm ngoài ở miền ngoài của tam giác.

Phương pháp giải - Xem chi tiết

Sử dụng:

\({S_q} =\dfrac {{\pi {R^2}n}}{ {360}}\)

Diện tích hình viên phân: \(S = {S_q} - {S_{AOB}}\)

Lời giải chi tiết

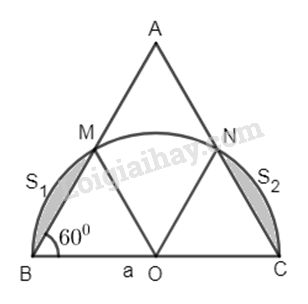
Gọi M, N lần lượt là giao điểm của nửa đường tròn đường kính BC với hai cạnh AB và AC.

∆BOM cân có \(\widehat B = 60^\circ \) nên là tam giác đều.

 và \(OB = \dfrac{a}{2}\)

Do đó diện tích hình quạt tròn BOM là :

\({S_q} =\dfrac {{\pi {R^2}n}}{ {360}} = \dfrac{{\pi {{\left( {\dfrac{a }{ 2}} \right)}^2}.60}}{ {360}} = \dfrac{{\pi {a^2}} }{ {24}}\)(đvdt)

\({S_{BOM}} = \dfrac{{{{\left( {{a \over 2}} \right)}^2}.\sqrt 3 }}{ 4} =\dfrac {{{a^2}.\sqrt 3 } }{ {16}}\)(đvdt)

Vậy \({S_1} = {S_q} - {S_{BOM}} = \dfrac{{\pi {a^2}} }{ {24}} -\dfrac {{{a^2}\sqrt 3 } }{ {16}} \)\(\,= \dfrac{{{a^2}\left( {2\pi  - 3\sqrt 3 } \right)}}{ {48}}\)

Dễ thấy S1 = S2.

Vậy diện tích phần hình tròn nằm ngoài của tam giác là : \(S =\dfrac {{2.{a^2}\left( {2\pi  - 3\sqrt 3 } \right)} }{{48}}\)\(\, = \dfrac{{{a^2}\left( {2\pi  - 3\sqrt 3 } \right)} }{ {24}}\).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store