Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 10. Diện tích hình tròn, hình quạt tròn

Bài 85 trang 100 SGK Toán 9 tập 2


Hình viên phân là hình tròn

Đề bài

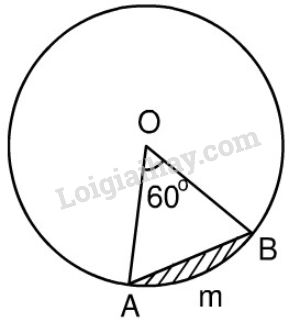
Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân \(AmB\), biết góc ở tâm \(\widehat {AOB} = {60^0}\) và bán kính đường tròn là \(5,1 cm\) (h.64)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Diện tích hình viên phân = Diện tích cung tròn \(AmB\) - Diện tích tam giác \(OAB.\)

+) Diện tích quạt tròn bán kính \(R\) và có số đo cung \(n^0\) là \(S=\dfrac {\pi R^2 n}{360}\)

Lời giải chi tiết

\(∆OAB\) là tam giác đều có cạnh bằng \(R = 5,1cm\).

Áp dụng công thức tính diện tích tam giác đều cạnh \(a\) là \(\displaystyle {{{a^2}\sqrt 3 } \over 4}\) ta có 

 \(\displaystyle {S_{\Delta OBA}} ={{{R^2}\sqrt 3 } \over 4}\)           (1)

Diện tích hình quạt tròn \(AOB\) là:

 \(\displaystyle {{\pi .{R^2}{{.60}^0}} \over {{{360}^0}}} = {{\pi {R^2}} \over 6}\)      (2)

Từ (1) và (2) suy ra diện tích hình viên phân là:

\(\displaystyle {{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {R^2}\left( {{\pi  \over 6} - {{\sqrt 3 } \over 4}} \right)\)

Thay \(R = 5,1\) ta có \(S\)viên phân ≈\( 2,4\) \((cm^2)\)

Loigiaihay.com


Bình chọn:
4.5 trên 48 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua