Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 10. Diện tích hình tròn, hình quạt tròn

Bài 82 trang 99 SGK Toán 9 tập 2


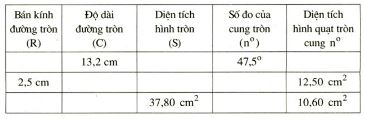
Điền vào ô trống trong bảng sau

Đề bài

Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất)

 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Độ dài đường tròn bán kính \(R\) là: \(C=2\pi R.\)

+) Độ dài cung tròn \(n^0\) của đường tròn bán kính \(R\) là: \(l = \dfrac{{\pi Rn}}{{180}}.\)

+) Diện tích hình tròn bán kính \(R\) là: \(S=\pi R^2.\)

+) Diện tích cung tròn \(n^0\) của đường tròn bán kính \(R\) là: \(S = \dfrac{{\pi R^2n}}{{360}}.\)

Lời giải chi tiết

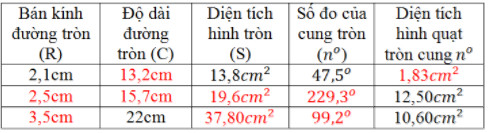
- Dòng thứ nhất:

 \( R\) = \(\dfrac{C}{2\pi }\) = \(\dfrac{13,2}{2. 3,14 }\) \(≈ 2,1\) (\(cm\))

\(S = π. R^2 = 3,14.{(2,1)}^2 ≈ 13,8 \)(\(cm^2\))

\({S_{quạt}}\)\(=\dfrac{\pi R^{2}n^{\circ}}{360^{\circ}}\) \(=\dfrac{3,14 .2,1^{2}.47,5}{360}\) \(≈ 1,83\)  (\(cm^2\))

- Dòng thứ hai:

\(C = 2πR = 2. 3,14. 2,5 = 15,7\) (cm)

\(S = π. R^2 = 3,14.{(2,5)}^2 ≈ 19,6\) (\(cm^2\))

\(n^0\)\(=\dfrac{S_{quat}.360^{\circ}}{\pi R^{2}}\)\(=\dfrac{12,5.360^{\circ}}{3,14.2,5^{2}}\)\(≈ 229,3^0\)  

- Dòng thứ ba:

\(R\) \(=\sqrt{\dfrac{s}{\pi }}\)  \(=\sqrt{\dfrac{37,8}{3,14 }}\) \(≈ 3,5\) (\(cm\))

\(C = 2πR = 22\) (\(cm\))

\(n^0\)\(=\dfrac{S_{quạt}.360^{\circ}}{\pi R^{2}}\) \(=\dfrac{10,6.360^{\circ}}{3,14.3,5^{2}}\) \(≈ 99,2^0\)  

Điền vào các ô trống ta được các bảng sau:


Bình chọn:
4.2 trên 66 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store