-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 1: Đo góc và cung
Bài 8 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho hai đường tròn đồng tâm (O; R) và
Đề bài
Cho hai đường tròn đồng tâm (O; R) và (O; \(\dfrac{{R\sqrt 3 }}{2}\)). Tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.
Phương pháp giải - Xem chi tiết
Sử dụng các hàm lượng giác, tính số đo góc \(\widehat {AOB}\).
Lời giải chi tiết
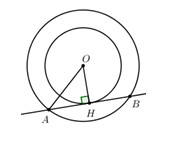
Xét tam giác vuông OAH có: \(OA = R;\,\,OH = \dfrac{{R\sqrt 3 }}{2}\)
\( \Rightarrow \cos \widehat {HOA} = \dfrac{{OH}}{{OA}} = \dfrac{{\dfrac{{R\sqrt 3 }}{2}}}{R} = \dfrac{{\sqrt 3 }}{2} \)\(\;\Rightarrow \widehat {HOA} = {30^0}\)
Chứng minh tương tự ta có \(\widehat {HOB} = {30^0}\).
Vậy \(\widehat {AOB} = {30^0} + {30^0} = {60^0} \) \(\Rightarrow sd\,cung\,AB = {60^0}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 10 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 11 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 12 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 13 trang 80 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
