-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 1: Đo góc và cung
Bài 3 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho hai đường tròn đồng tâm
Đề bài
Cho hai đường tròn đồng tâm \(\left( {O;R} \right)\); \(\left( {O;r} \right)\)với (R > r). Lấy điểm M ở ngoài hai đường tròn, qua M vẽ hai tiếp tuyến với \(\left( {O;r} \right)\), chúng lần lượt cắt \(\left( {O;R} \right)\)tại A, B và C, D. Chứng minh cung AB = cung CD
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất:
+) Hai dây cách đều tâm thì bằng nhau.
+) Hai dây bằng nhau căng hai cung bằng nhau.
Lời giải chi tiết
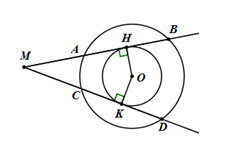
Gọi H, K lần lượt là các tiếp điểm của tiếp tuyến kẻ từ M đối với đường tròn \(\left( {O;r} \right)\) ta có \(OH = OK = r\)
\( \Rightarrow AB = CD\) (hai dây cách đều tâm thì bằng nhau)
cung AB = cung CD (hai dây bằng nhau căng hai cung bằng nhau).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 5 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 6 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 7 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 8 trang 79 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
