-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 1: Đo góc và cung
Bài 10 trang 79 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Hai đường tròn (O; r) và (O’ ; R) cắt nhau tại hai điểm phân biệt A và B. Vẽ đường kính BOC và
Đề bài
Hai đường tròn (O; r) và (O’ ; R) cắt nhau tại hai điểm phân biệt A và B. Vẽ đường kính BOC và BO’D. Cho biết R > r, hãy so sánh hai cung AC và AD của hai đường tròn.
Phương pháp giải - Xem chi tiết
+) Sử dụng tính chất: Tam giác cân có 2 góc ở đáy bằng nhau, tính số đo góc \(\widehat {AOC}\) theo \(\widehat {OCA}\).
+) Tương tự tính góc \(\widehat {AO'D}\) theo \(\widehat {O'DA}\).
+) Sử dụng định lí: Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn so sánh hai góc \(\widehat {OCA}\) và \(\widehat {O'DA}\), từ đó rút ra kết luận.
Lời giải chi tiết
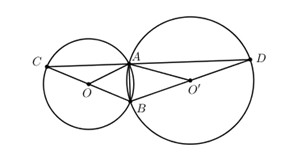
Xét tam giác OAC có \(OA = OC = r \Rightarrow \Delta OAC\) cân tại O \( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Ta có: \(\widehat {AOC} + \widehat {OAC} + \widehat {OCA} = {180^0}\)
\(\Rightarrow \widehat {AOC} = {180^0} - \left( {\widehat {OAC} + \widehat {OCA}} \right) = {180^0} - 2\widehat {OCA}\)
Chứng minh hoàn toàn tương tự ta có: \(\widehat {AO'D} = {180^0} - 2\widehat {O'DA}\).
Vì \(r < R \Rightarrow 2r < 2R \Rightarrow BC < BD\)
Xét tam giác BCD có \(BC < BD \Rightarrow \widehat {O'DA} < \widehat {OCA}\) (Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn).
\( \Rightarrow - 2\widehat {O'DA} > - 2\widehat {OCA} \)
\(\Leftrightarrow {180^0} - 2\widehat {O'DA} > {180^0} - 2\widehat {OCA}\)
\(\Leftrightarrow \widehat {AO'D} > \widehat {AOC}\)
Vậy sđ cung AD > sđ AC (đpcm).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 11 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 12 trang 79 Tài liệu dạy – học Toán 9 tập 2
- Bài 13 trang 80 Tài liệu dạy – học Toán 9 tập 2
- Bài 14 trang 80 Tài liệu dạy – học Toán 9 tập 2
- Bài 15 trang 80 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
