Bài 53 trang 87 SGK Toán 8 tập 2

Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m.

Đề bài

Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao \(2m\) và đặt xa cây \(15m\). Sau khi người ấy lùi ra xa cách cọc \(0,8m\) thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân tới mắt người ấy là \(1,6m\)?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Áp dụng tính chất hai tam giác đồng dạng.

- Định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Lời giải chi tiết

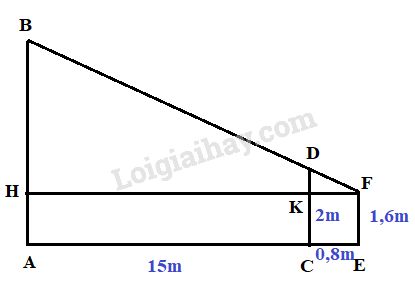
Giả sử \(AB\) là cây cần đo, \(CD\) là cọc \(EF\) là khoảng cách từ mắt tới chân.

Ta có: \(AC=15m, CE=0,8m, EF=1,6m, CD=2m\) và \(HACK, CEFK\) là các hình chữ nhật.

Ta có: \(KD // HB\) (giả thiết)

\( \Rightarrow ∆KDF ∽ ∆HBF\) (Theo định lí)

\(\Rightarrow \dfrac{HB}{KD}= \dfrac{HF}{KF}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow HB.KF=KD.HF\)

\( \Rightarrow HB = \dfrac{HF.KD}{KF}\)

Mà \(HF = HK + KF =AC + CE\) \( = 15 + 0,8 = 15,8m \)

\(KD = CD - CK = CD - EF \) \(= 2 - 1,6 = 0,4 m\)

Do đó: \(HB = \dfrac{15,8 . 0,4}{0,8 }= 7,9 m \)

Vậy chiều cao của cây là \(AB = HB + AH = 7,9 + 1,6 = 9,5 m\).

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 147 phiếu

Bài tiếp theo

Bài 54 trang 87 SGK Toán 8 tập 2
Giải bài 54 trang 87 SGK Toán 8 tập 2. Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách như hình 57:
Bài 55 trang 87 SGK Toán 8 tập 2
Giải bài 55 trang 87 SGK Toán 8 tập 2. Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm.

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý