Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học

Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông

Đề kiểm tra 45 phút - Đề số 6 - Chương 1 - Hình học 9

Giải Đề kiểm tra 45 phút - Đề số 6 - Chương 1 - Hình học 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Bài 1. Tính giá trị của biểu thức :

$A = {{3\cot 77^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ + {{\cos }^2}64^\circ - {{\cos }^2}71^\circ - {{\cos }^2}19^\circ } \over {{{\sin }^2}34^\circ + {{\sin }^2}56^\circ + {{\sin }^2}15^\circ + {{\sin }^2}75^\circ }}$

Bài 2. Cho hình thang ABCD (AB // CD) có $AB = 1cm$ , $CD = 5cm$ và $\widehat C = 30^\circ ,\widehat D = 60^\circ$ . Tính diện tích hình thang ABCD.

Bài 3. Cho tam giác ABC có ba góc nhọn, các đường cao BI, CK cắt nhau tại H. Trên đoạn HB, HC lần lượt lấy các điểm D và E sao cho $\widehat {ADC} = \widehat {AEB} = 90^\circ .$

a. Chứng minh rằng ∆ADE cân

b. Cho $AD = 6cm, AC = 10cm$ . Tính DC, CI và diện tích $∆ADI.$

LG bài 1

Phương pháp giải:

Sử dụng:

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

${\sin ^2}\alpha + {\cos ^2}\alpha = 1$

Lời giải chi tiết:

Ta có:

$\eqalign{ A &= {{3\cot 77^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ + {{\cos }^2}64^\circ - {{\cos }^2}71^\circ - {{\cos }^2}19^\circ } \over {{{\sin }^2}34^\circ + {{\sin }^2}56^\circ + {{\sin }^2}15^\circ + {{\sin }^2}75^\circ }} \cr & = {{3\tan 13^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ + {{\sin }^2}26^\circ - {{\cos }^2}71^\circ - {{\sin }^2}71^\circ } \over {{{\sin }^2}34^\circ + {{\cos }^2}34^\circ + {{\sin }^2}15^\circ + {{\cos }^2}15^\circ }} \cr & = {3 \over 2} - {{1 - \left( {{{\cos }^2}71^\circ + {{\sin }^2}71^\circ } \right)} \over {1 + 1}}\cr& = {3 \over 2} - {{1 - 1} \over 2} = {3 \over 2} \cr}$

LG bài 2

Phương pháp giải:

* Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

+) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

+) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

* Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

Lời giải chi tiết:

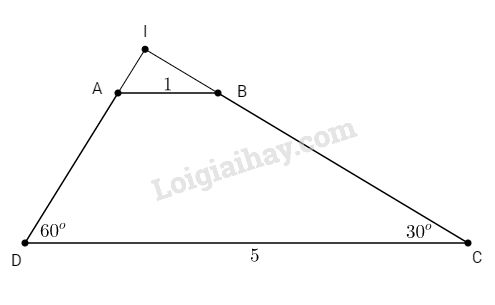
Gọi I là giao điểm của CB và DA

Khi đó ∆ICD vuông tại I (vì $\widehat C + \widehat D = 30^\circ + 60^\circ = 90^\circ$ ) và $ID = {1 \over 2}CD$ (trong tam giác vuông cạnh đối diện góc 30˚ bằng nửa cạnh huyền).

Mặt khác ∆ICD vuông tại I, ta có:

$IC = CD.\sin D = 5.\sin 60^\circ = {{5\sqrt 3 } \over 2}\,\left( {cm} \right)$

Do đó: ${S_{ICD}} = {1 \over 2}IC.ID = {1 \over 2}.{{5\sqrt 3 } \over 2}.{5 \over 2} = {{25\sqrt 3 } \over 8}\,\left( {c{m^2}} \right)$

Vì AB // CD (gt) nên:

$\widehat {IAB} = \widehat D = 60^\circ$ (đồng vị)

và $\widehat {IBA} = \widehat C = 30^\circ$

Tương tự, trong ∆IAB vuông tại I, ta có:

$\eqalign{ & IA = AB.\sin 30^\circ = 1.\sin 30^\circ = {1 \over 2}\,\left( {cm} \right) \cr & va\,IB = AB.\cos 30^\circ = 1.\cos 30^\circ = {{\sqrt 3 } \over 2}\,\left( {cm} \right) \cr}$

Do đó: ${S_{IAB}} = {1 \over 2}IA.IB = {1 \over 2}.{1 \over 2}.{{\sqrt 3 } \over 2} = {{\sqrt 3 } \over 8}\,\left( {c{m^2}} \right)$

Ta có: ${S_{ABCD}} = {S_{ICD}} - {S_{IAB}}$ $\;= {{25\sqrt 3 } \over 8} - {{\sqrt 3 } \over 8} = {{24\sqrt 3 } \over 8} = 3\sqrt 3 \,\left( {c{m^2}} \right)$

LG bài 3

Phương pháp giải:

Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có các hệ thức sau:

+) $A{B^2} = BH.BC$ và $A{C^2} = CH.BC$

+) $H{A^2} = HB.HC$

+) $AB.AC = BC.AH$

+) $B{C^2} = A{B^2} + A{C^2}$ (Định lí Pitago).

Lời giải chi tiết:

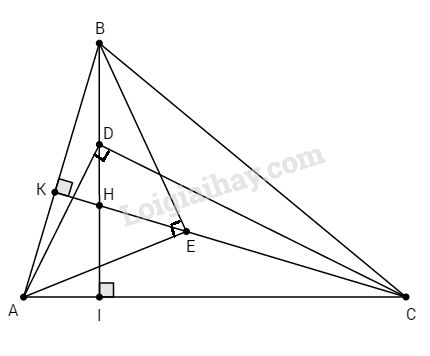
a. Ta có: ∆ADC vuông tại D, đường cao DI nên :

$A{D^2} = AC.AI$ (định lí 1) (1)

Tương tự: ∆AEB có đường cao EK:

$A{E^2} = AB.AK$ (2)

Dễ thấy ∆AIB đồng dạng ∆AKC (g.g)

$\eqalign{ & \Rightarrow {{AB} \over {AC}} = {{AI} \over {AK}} \cr & \Rightarrow AB.AK = AC.AI\,\left( 3 \right) \cr}$

Từ (1), (2) và (3) $\Rightarrow A{D^2} = A{E^2}$

Vậy ∆ADE cân tại E.

b. Ta có: ∆ADC vuông :

$DC = \sqrt {A{C^2} - A{D^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,\left( {cm} \right)$

Lại có DI là đường cao của tam giác vuông ADC, ta có:

$C{D^2} = CA.CI$ (định lí 1)

$\Rightarrow CI = {{C{D^2}} \over {CA}} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)$

Do đó: $AI = AC – CI = 10 – 6,4 = 3,6 (cm)$

Ta có: $DI.CA = DA.DC$ (định lí 3)

$\Rightarrow DI = {{DA.DC} \over {AC}} = {{6.8} \over {10}} = 4,8\,\left( {cm} \right)$

Vậy ${S_{ADI}} = {1 \over 2}AI.DI = {1 \over 2}.3,6.4,8 = 8,64\,\left( {c{m^2}} \right)$

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 12 phiếu

Bài tiếp theo

Đề kiểm tra 45 phút - Đề số 5 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 5 - Chương 1 - Hình học 9
Đề kiểm tra 45 phút - Đề số 4- Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 4 - Chương 1 - Hình học 9
Đề kiểm tra 45 phút - Đề số 3 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 3 - Chương 1 - Hình học 9
Đề kiểm tra 45 phút - Đề số 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 2 - Chương 1 - Hình học 9
Đề kiểm tra 45 phút - Đề số 1 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 1 - Chương 1 - Hình học 9
Lý thuyết Ôn tập chương 1. Hệ thức lượng trong tam giác vuông
Lý thuyết Ôn tập chương 1. Hệ thức lượng trong tam giác vuông
Bài 43 trang 96 SGK Toán 9 tập 1
Từ hai quan sát trên, em hãy tính xấp xỉ “chu vi” Trái Đất.
Bài 42 trang 96 SGK Toán 9 tập 1
Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường bao nhiêu mét để đảm bảo an toàn.
Bài 41 trang 96 SGK Toán 9 tập 1
Giải bài 41 trang 96 SGK Toán 9 tập 1. Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, . Dùng các thông tin sau (nếu cần) để tìm x – y
Bài 40 trang 95 SGK Toán 9 tập 1
Tính chiều cao của cây trong hình 50 (làm tròn đến đề - xi – mét)
Bài 39 trang 95 SGK Toán 9 tập 1
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
Bài 38 trang 95 SGK Toán 9 tập 1
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48.
Bài 37 trang 94 SGK Toán 9 tập 1
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
Bài 36 trang 94 SGK Toán 9 tập 1
Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm.
Bài 35 trang 94 SGK Toán 9 tập 1
Tỉ số giữa hai cạnh góc vuông của một hình tam giác vuông bằng 19 : 28. Tìm các góc của nó.
Bài 34 trang 93 SGK Toán 9 tập 1
Chọn kết quả đúng trong các kết quả dưới đây:
Bài 33 trang 93 SGK Toán 9 tập 1
Chọn kết quả đúng trong các kết quả dưới đây:
Trả lời phần câu hỏi ôn tập chương 1 phần Hình học trang 91 SGK toán 9 tập 1
Cho hình 36. Hãy viết hệ thức giữa: a)Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.