 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
Đề kiểm tra 45 phút - Đề số 1 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 1 - Chương 1 - Hình học 9
Đề bài
Bài 1. a. Không sử dụng máy tính, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: \(sin{78^o},{\rm{ }}cos{24^o},{\rm{ }}sin{40^o},{\rm{ }}cos{87^o},{\rm{ }}sin{42^o}\)
b. Tính : \(D = {\sin ^2}15^\circ + {\sin ^2}75^\circ - {{2\cos 49^\circ } \over {\sin 41^\circ }} \)\(\,+ \tan 26^\circ .\tan 64^\circ \)
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH, \(AC = 3cm,HC = 1,8cm.\)
a. Giải tam giác ABC
b. Tính độ dài phân giác AD của tam giác ABC (số đo góc làm tròn đến phút, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ hai)
Bài 3. Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC.
a. Chứng minh \(AM.AB = AN.AC\).
b. Chứng minh \({{{S_{AMN}}} \over {{S_{ABC}}}} = {\sin ^2}B.{\sin ^2}C\)
LG bài 1
Phương pháp giải:
Sử dụng:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Khi góc α tăng từ 0° đến 90° (0°<α < 90°) thì sinα và tgα tăng còn cosα và cotgα giảm.
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Lời giải chi tiết:
a. Ta có: \(\cos 24^\circ = \sin 66^\circ ,\cos 87^\circ = \sin 3^\circ .\)
Vì \(3^\circ < 40^\circ < 42^\circ < 66^\circ < 78^\circ \) nên:
\(\eqalign{ & \sin 3^\circ < \sin 40^\circ < \sin 42^\circ < \sin 78^\circ \cr & \Rightarrow \cos 87^\circ < \sin 40^\circ < \sin 42^\circ < \cos 24^\circ < \sin 78^\circ \cr} \)
b.
\(\eqalign{ D &= {\sin ^2}15^\circ + {\sin ^2}75^\circ - {{2\cos 49^\circ } \over {\sin 41^\circ }} + \tan 26^\circ .\tan 64^\circ \cr & = {\sin ^2}15^\circ + {\cos ^2}15^\circ - {{2\sin 41^\circ } \over {\sin 41^\circ }} + \tan 26^\circ .\cot 26^\circ \cr&= 1 - 2 + 1 = 0 \cr} \)
LG bài 2
Phương pháp giải:
Sử dụng:
Định lý Pytago
Hệ thức lượng trong tam giác vuông
Tỉ số lượng giác của góc nhọn
Tính chất đường phân giác của tam giác
Lời giải chi tiết:
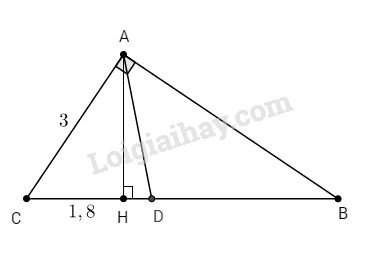
a. ∆ABC vuông tại A có đường cao AH, ta có:
\(A{C^2} = BC.HC\) (hệ thức lượng)
\( \Rightarrow BC = {{A{C^2}} \over {HC}} = {{{3^2}} \over {1,8}} = 5\) (cm)
Theo định lí Py-ta-go, ta có:
\(A{B^2} = B{C^2} - A{C^2} = {5^2} - {3^2} = 16 \)
\(\Rightarrow AB = 4\,\left( {cm} \right)\)
Ta có: \(\eqalign{ & \sin B = {{AC} \over {BC}} = {3 \over 5} \Rightarrow \widehat B \approx 36^\circ 52' \cr & \Rightarrow \widehat C \approx 90^\circ - 36^\circ 52' \approx 53^\circ 08' \cr} \)
b. AD là phân giác của ∆ABC, ta có:
\(\eqalign{ & {{DB} \over {DC}} = {{AB} \over {AC}} = {4 \over 3}\cr& \Rightarrow {{DB} \over 4} = {{DC} \over 3} = {{DB + DC} \over {4 + 3}} = {{BC} \over 7} = {5 \over 7} \cr & \Rightarrow DB = {{4.5} \over 7} = {{20} \over 7}\,\left( {cm} \right) \cr} \)
Ta có: \(\eqalign{ & BH = BC - HC = 5 - 1,8 = 3,2\,\left( {cm} \right) \cr & \Rightarrow DH = BH - BD = 3,2 - {{20} \over 7} \approx 0,34\,\left( {cm} \right) \cr} \)
Lại có: \(BC.AH = AB.AC\) (hệ thức lượng)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{3.4} \over 5} = 2,4\,\left( {cm} \right)\)
Áp dụng định lí Pi-ta-go trong tam giác vuông AHD, ta có:
\(A{D^2} = A{H^2} + D{H^2}\)\(\; \approx {\left( {2,4} \right)^2} + {\left( {0,34} \right)^2} \approx 5,8756\)
\(\Rightarrow AD \approx 2,42\,\left( {cm} \right)\)
LG bài 3
Phương pháp giải:
Sử dụng:
Hệ thức lượng trong tam giác vuông
Tỉ số lượng giác của góc nhọn
Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng
Lời giải chi tiết:
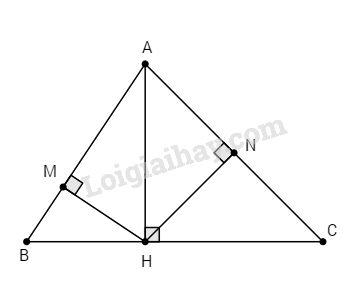
a. \(∆AHB\) vuông tại H (giả thiết) có HM là đường cao, ta có:
\(A{H^2} = AM.AB\) (hệ thức lượng) (1)
Tương tự với \(∆AHC\) có đường cao HN, ta có:
\(A{H^2} = AN.AC\) (2)
Từ (1) và (2) \(⇒ AM.AB = AN.AC\) (3)
b. Xét \(∆AMN\) và \(∆ABC\) có \(\widehat A\) chung và (3)
\(⇒ ∆AMN\) đồng dạng \(∆ACB\) (c.g.c)
\( \Rightarrow {{{S_{AMN}}} \over {{S_{ACB}}}} = {\left( {{{AN} \over {AB}}} \right)^2}\) (4)
Ta có: \({\widehat H_1} = \widehat C\) (cùng phụ với \({\widehat H_2}\) )
Xét \(∆ANH\) vuông tại N, ta có:
\(AN = AH.sin{H_1} = AH.sinC\) (vì \({\widehat H_1} = \widehat C\) )
\( \Rightarrow A{N^2} = A{H^2}.{\sin ^2}C\) (5)
Xét \(∆AHB\), ta có: \(AH = AB.\sin B \Rightarrow {\rm A}{{\rm H}^2} = A{B^2}.{\sin ^2}B\)
\( \Rightarrow A{B^2} = {{A{H^2}} \over {{{\sin }^2}B}}\) (6)
Thay (5), (6) vào (4), ta có: \({{{S_{AMN}}} \over {{S_{ACB}}}} = {{A{H^2}.{{\sin }^2}C} \over {{{A{H^2}} \over {{{\sin }^2}B}}}} = {\sin ^2}B.{\sin ^2}C\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận