Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 1 - Hình học 9
Đề bài
Bài 1. Cho góc nhọn \(α\), biết \(\sin \alpha = {2 \over 3}.\) Không tính số đo góc \(α\), hãy tính \(\cos α, \tanα, \cotα.\)
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, BH = 5cm, chứng minh rằng : tanB = 3tanC.
LG bài 1
Phương pháp giải:
Sử dụng:
\(\begin{array}{l}
{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\
\tan \alpha .\cot \alpha = 1
\end{array}\)
Lời giải chi tiết:
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
\(\Rightarrow \cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } = \sqrt {1 - {{\left( {{2 \over 3}} \right)}^2}}\)\(\, = {{\sqrt 5 } \over 3}\)
\(\tan \alpha = {{\sin \alpha } \over {\cos \alpha }} = {2 \over 3}:{{\sqrt 5 } \over 3} = {{2\sqrt 5 } \over 5} \)
\(\Rightarrow \cot \alpha = \frac{1}{{\tan \alpha }} = {{\sqrt 5 } \over 2}\)
LG bài 2
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn.
Lời giải chi tiết:
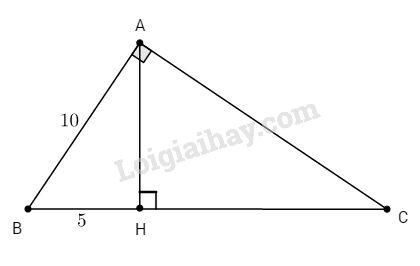
Ta có: \(∆ABC\) vuông, có đường cao AH
\( \Rightarrow A{B^2} = BC.BH\)
\(\Rightarrow BC = {{A{B^2}} \over {BH}} = {{{{10}^2}} \over 5} = 20\) (cm)
Do đó: \(HC = BC - BH = 20 - 5 = 15\,\left( {cm} \right)\)
\(∆AHB\) vuông có: \(\tan B = {{AH} \over {BH}} = {{AH} \over 5}\)
\(∆AHC\) vuông có: \(\tan C = {{AH} \over {CH}} = {{AH} \over {15}}\)
Do đó \({{\tan B} \over {\tan C}} = {{AH} \over 5}:{{AH} \over {15}} = 3 \)
\(\Rightarrow \tan B = 3\tan C\)
Loigiaihay.com
Các bài khác cùng chuyên mục












