Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 9
Đề bài
Bài 1. Cho \(\tan α = 3\). Tính \({{\cos \alpha + sin\alpha } \over {\cos \alpha - \sin \alpha }}\)
Bài 2. Cho \(∆ABC\) có góc A nhọn. Chứng minh rằng : \({S_{ABC}} = {1 \over 2}AB.AC.\sin A\)
LG bài 1
Phương pháp giải:
Sử dụng \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
Lời giải chi tiết:
Đặt \(A = {{\cos \alpha + \sin \alpha } \over {\cos \alpha - \sin \alpha }}.\) Chia cả tử và mẫu của A cho \(\cos α\), ta có:
\(A = \dfrac{{\dfrac{{\cos \alpha }}{{\cos \alpha }} + \dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\dfrac{{\cos \alpha }}{{\cos \alpha }} - \dfrac{{\sin \alpha }}{{\cos \alpha }}}}\)\( = {{1 + \tan \alpha } \over {1 - \tan \alpha }}\)
Thay \(\tan α = 3\), ta có: \(A={{1 + 3} \over {1 - 3}} = {4 \over { - 2}} = - 2\)
LG bài 2
Phương pháp giải:
Sử dụng \(\sin \alpha = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}}\)
Diện tích tam giác bằng nửa tích cạnh đáy với chiều cao tương ứng.
Lời giải chi tiết:
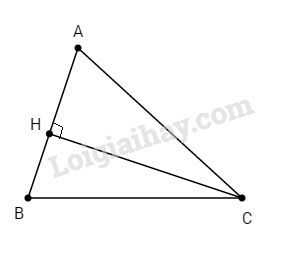
Vẽ \(CH ⊥ AB\), ta có:
\(\eqalign{ & \sin A = {{CH} \over {CA}} \Rightarrow CH = AC.\sin A \cr & {S_{ABC}} = {1 \over 2}AB.CH \cr&\;\;\;\;\;\;\;\;\;= {1 \over 2}AB.AC.\sin A. \cr} \)
Loigiaihay.com
Các bài khác cùng chuyên mục













Danh sách bình luận