Bài 89 trang 111 SGK Toán 8 tập 1
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AB, E\) là điểm đối xứng với \(M\) qua \(D\).
a) Chứng minh rằng điểm \(E\) đối xứng với điểm \(M\) qua \(AB\).
b) Các tứ giác \(AEMC, AEBM\) là hình gì? Vì sao?
c) Cho \(BC = 4cm\), tính chu vi tứ giác \(AEBM\).
d) Tam giác vuông \(ABC\), có điều kiện gì thì \(AEBM\) là hình vuông?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
- Hình bình hành có hai đường chéo vuông góc là hình thoi.
- Hình thoi có một góc vuông là hình vuông.
Lời giải chi tiết
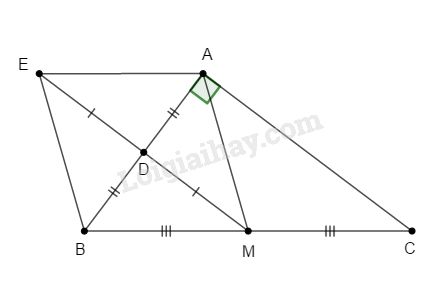
a) Ta có \(MB = MC\) (vì \(M\) là trung điểm của \(BC\) ),
\(BD = DA\) (vì \(D\) là trung điểm của \(AB\) )
nên \(MD\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)
Do đó \(MD // AC,MD=\dfrac{AC}2\) (tính chất đường trung bình của tam giác)
Do \(AC ⊥ AB\) (gt) nên \(MD ⊥ AB\)
Vì \(E\) là điểm đối xứng với \(M\) qua \(D\) nên \(D\) là trung điểm của \(EM\) hay \(DE=DM\)
Do đó, \(AB\) là đường trung trực của \(ME\) (do \(AB ⊥ ME\) tại \(D\) và \(DE = DM\)) nên \(E\) đối xứng với \(M\) qua \(AB\).
b) Ta có: \(EM // AC\) (do \(MD // AC\))
và \(EM = AC\) (cùng bằng \(2DM\))
Suy ra \(AEMC\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Tứ giác \(AEBM\) có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành.
Hình bình hành \(AEBM\) có \(AB ⊥ EM\) (chứng minh trên) nên \(AEBM\) là hình thoi (dấu hiệu nhận biết hình thoi)
c) Ta có \(BC = 4 cm \Rightarrow BM = 2 cm\) (do \(M\) là trung điểm \(BC\))
Chu vi hình thoi \(AEBM\) bằng \(4.BM = 4. 2 = 8(cm)\)
d) Cách 1:
Hình thoi \(AEBM\) là hình vuông \(⇔ AB = EM ⇔ AB = AC\)
Vậy nếu \(ABC\) vuông có thêm điều kiện \(AB = AC\) (tức là tam giác \(ABC\) vuông cân tại \(A\)) thì \(AEBM\) là hình vuông.
Cách 2 :
Hình thoi \(AEBM\) là hình vuông \(⇔AM ⊥ BM\)
\(⇔∆ABC\) có trung tuyến \(AM\) là đường cao
\(⇔∆ABC\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)
Vậy nếu \(∆ABC\) vuông có thêm điều kiện cân tại \(A\) thì \(AEBM\) là hình vuông.













Danh sách bình luận