Bài 51 trang 87 SGK Toán 9 tập 2
Cho I, O lần lượt là tâm đường tròn
Đề bài
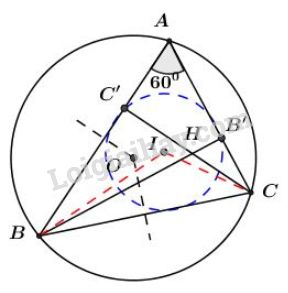
Cho \(I, \, O\) lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác \(ABC\) với \(\widehat{A} = 60^0.\) Gọi \(H\) là giao điểm của các đường cao \(BB'\) và \(CC'.\)
Chứng minh các điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)
Nên ta chỉ ra \(\widehat{BOC}=\widehat{BHC}=\widehat{BIC}\).
Lời giải chi tiết
+) Ta có: \(\widehat{BOC} = 2\widehat{BAC} = 2.60^0= 120^0\) (góc nội tiếp và góc ở tâm cùng chắn một cung \(BC\)). (1)
+) Lại có \(\widehat{BHC} = \widehat{B'HC'}\) (hai góc đối đỉnh)
Xét tứ giác AB'HC' có: \(\widehat{B'HC'} + \widehat {HC'A} + \widehat {HB'A} + \widehat A = 360^0\) (tổng các góc của tứ giác bằng \(360^0\)) nên \(\widehat{B'HC'} = 360^\circ - \widehat {HC'A} - \widehat {HB'A} - \widehat A\) \( = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ\)
\(\Rightarrow \widehat{BHC} = 120^0.\) (2)
+) Vì I là tâm đường tròn nội tiếp tam giác ABC nên BI; CI lần lượt là tia phân giác góc B, góc C.
Xét tam giác \(ABC\) có \(\widehat B + \widehat C + \widehat A = 180^\circ \) (Định lí tổng 3 góc trong một tam giác) \( \Leftrightarrow \widehat B + \widehat C = 180^\circ - 60^\circ = 120^\circ \)
Xét tam giác BIC có \(\widehat {BIC}+ \widehat {IBC}+ \widehat {ICB}=180^0\) (Định lí tổng 3 góc trong một tam giác)
\(\Rightarrow \)\(\begin{array}{l}\widehat {BIC} = 180^\circ - \widehat {IBC} - \widehat {ICB} = 180^\circ - \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}\\ = 180^\circ - \dfrac{{\widehat B + \widehat C}}{2} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Do đó \(\widehat{BIC} = 120^0.\) (3)
Từ (1), (2), (3) ta thấy các điểm \(O, \, H, \, I\) cùng nằm trên các cung chứa góc \(120^0\) dựng trên đoạn thẳng \(BC.\) hay 5 điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn.
Các bài khác cùng chuyên mục













Danh sách bình luận