Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 2 : Góc chắn cung

Bài 18 trang 95 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Trên đường tròn (O) lấy các điểm A và A’ sao cho sđ cung AA’ = 1200. Điểm B trên cung nhỏ ,

Đề bài

Trên đường tròn (O) lấy các điểm A và A’ sao cho sđ cung AA’ = 1200. Điểm B trên cung nhỏ , điểm C trên cung lớn AA’ sao cho sđ cung AC= 2 sđ cung AB

a) Chứng minh \(\widehat {ACB} = \dfrac{{\widehat {ABC}}}{2}\) .

b) \(\widehat {A'BC} = 2\widehat {A'CB}\)

c) Gọi B là điểm chính giữa cung nhỏ AA’ và I là một điểm trên cung nhỏ BA’. J là giao điểm của BI và AA’. Chứng minh \(\widehat {BJA'} = \widehat {IA'B}\) .

Phương pháp giải - Xem chi tiết

+) Số đo góc nội tiếp bằng nửa số đo cung bị chắn.

+) Số đo góc có đỉnh ở ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn (cung lớn trừ cung nhỏ).

Lời giải chi tiết

 

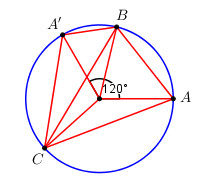
a) Ta có: \(sdcung\,AC < {180^0}\) \( \Rightarrow sdcung\,AB < {90^0}\).

Ta có: \(\widehat {ACB} = \dfrac{1}{2}sd\,cung\,AB;\,\,\widehat {ABC} = \dfrac{1}{2}sd\,cung\,AC\)  (số đo góc nội tiếp bằng nửa số đo cung bị chắn).

Mà  \(sd\,cung\,AC = 2sdcung\,AB\) \( \Rightarrow \widehat {ABC} = \dfrac{1}{2}.2sd\,cung\,AB = sd\,cung\,AB\)

\( \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2}\).

b) Ta có:

\(\begin{array}{l}sdcung\,A'B = sdAA' - sdcung\,AB = {120^0} - sdcung\,AB;\,\,\\
sdcung\,A'C = sdcung{\rm{ACA}}' - sdcung\,AC \\\;\;\;\;\;\;\;\;\;= {360^0} - {120^0} - sdcung\,AC\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {240^0} - sdcung\,AC \\\;\;\;\;\;\;\;\;\;\;= {240^0} - 2sdcung\,AB \\\;\;\;\;\;\;\;\;\;\;= 2\left( {{{120}^0} - sdcung\,AB} \right) \\\;\;\;\;\;\;\;\;\;= 2sdcung\,A'B\end{array}\)

Lại có

\(\begin{array}{l}\widehat {A'BC} = \dfrac{1}{2}sdcung\,A'C = \dfrac{1}{2}.2sdcung\,A'B = sdcung\,A'B;\,\,\\\widehat {A'CB} = \dfrac{1}{2}sdcung\,A'B\end{array}\)

(số đo góc nội tiếp bằng nửa số đo cung bị chắn).

Vậy \(\widehat {A'BC} = 2\widehat {A'CB}\).

c)

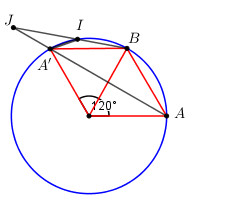
Vì B là điểm chính giữa cung nhỏ AA’ suy ra sđ cung AB= sđ cung A'B.

Vì \(\widehat {BJA'}\) là góc có đỉnh ở bên ngoài đường tròn nên 

\(\widehat {BJA'} = \dfrac{{sdcung\,AB - sdcung\,A'I}}{2}\)\(\, = \dfrac{{sdcung\,A'B - sdcung\,A'I}}{2}\)\(\, = \dfrac{{sdcung\,IB}}{2}\)

Vì \(\widehat {IA'B}\) là góc nội tiếp chắn cung IB nên .

Vậy \(\widehat {BJA'} = \widehat {IA'B}\).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store