Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 2 : Góc chắn cung

Bài 11 trang 94 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Từ điểm P ở ngoài đường tròn (O), vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Vẽ dây cung

Đề bài

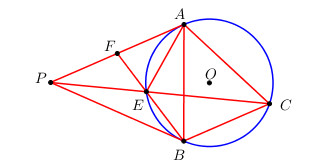
Từ điểm P ở ngoài đường tròn (O), vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Vẽ dây cung BC // PA. Gọi E là giao điểm thứ hai của PC với đường tròn (O) và F là giao điểm của BE và PA.

a) Chứng minh các cặp tam giác đồng dạng PFB và EFP, AFE và BFA.

b) Chứng minh PF = FA

Phương pháp giải - Xem chi tiết

a) Chứng minh các cặp tam giác đồng dạng theo trường hợp g-g.

b) Từ các cặp tam giác đồng dạng ở câu a), suy ra các tỉ số đồng dạng chứa cạnh PF và FA.

Lời giải chi tiết

 

a) +) Ta có \(\widehat {FPE} = \widehat {ECB}\) (so le trong bằng nhau do AP // BC);

Lại có: \(\widehat {EBC} = \widehat {FBP}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE)

\( \Rightarrow \widehat {FPE} = \widehat {FBP}\).

Xét \(\Delta PFB\) và \(\Delta EFP\) có:

\(\widehat {BFP}\) chung;

\(\widehat {FPE} = \widehat {FBP}\,\,\left( {cmt} \right);\)

 \( \Rightarrow \Delta PFB \sim \Delta EFP\,\,\left( {g.g} \right)\)

+) Xét \(\Delta AFE\) và \(\Delta BFA\) có:

\(\widehat {AFB}\) chung;

\(\widehat {EAF} = \widehat {ABF}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AE)

 \( \Rightarrow \Delta AFE \sim \Delta BFA\,\,\left( {g.g} \right)\)

b)  \(\Delta PFB \sim \Delta EFP\,\,\left( {cmt} \right)\)

\(\Rightarrow \dfrac{{PF}}{{EF}} = \dfrac{{BF}}{{PF}} \Rightarrow P{F^2} = EF.BF\) (1)

\(\Delta AFE \sim \Delta BFA\,\,\left( {cmt} \right) \)

\(\Rightarrow \dfrac{{FA}}{{BF}} = \dfrac{{EF}}{{FA}} \Rightarrow F{A^2} = EF.BF\)  (2)

Từ (1) và (2) \( \Rightarrow P{F^2} = F{A^2} \Rightarrow PF = FA\) (đpcm).

Loigiaihay.com


Bình chọn:
3.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store