Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Trả lời câu hỏi Bài 5 trang 111 SGK Toán 9 Tập 1


Hãy chứng minh cách dựng trên là đúng.

Đề bài

Hãy chứng minh cách dựng trên là đúng.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng:  Đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó là tiếp tuyến của đường tròn.

Lời giải chi tiết

 

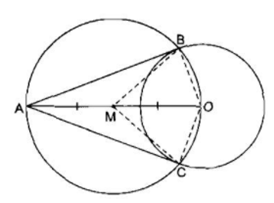
Ta có: MA = MO = MB ( cùng bằng bán kính đường tròn tâm M, bán kính MO)

\(MA{\rm{ }} = {\rm{ }}MB \Rightarrow \Delta MAB\) cân tại \(M \Rightarrow \widehat {BAO} = \widehat {ABM}\)

\(MO = MB \Rightarrow \Delta MOB\) cân tại \(M \Rightarrow \widehat {BOA}{\rm{ }} = \widehat {MBO}\)

\( \Rightarrow \widehat {BAO} + \widehat {BOA} = \widehat {ABM}{\rm{ }} + \widehat {MBO}{\rm{ }} = \widehat {ABO}{\rm{ }}\left( 1 \right)\)

Mặt khác ta lại có: \(\widehat {BAO} + \widehat {BOA} + \widehat {ABO} = {180^o}\,\,\,\,\left( 2 \right)\) (tổng 3 góc trong tam giác)

Từ (1) và (2) \( \Rightarrow \widehat {ABO} =180^0:2= {90^o}\)

Suy ra \(AB\bot BO\) tại \(B\), mà \(B\in (O)\)

Do đó AB là tiếp tuyến của (O) 

Chứng minh tương tự,

Ta có: MA = MO = MC ( cùng bằng bán kính đường tròn tâm M, bán kính MO)

\(MA{\rm{ }} = {\rm{ }}MC \Rightarrow \Delta MAC\) cân tại \(M \Rightarrow \widehat {CAO} = \widehat {ACM}\)

\(MO = MC \Rightarrow \Delta MOC\) cân tại \(M \Rightarrow \widehat {COA}{\rm{ }} = \widehat {MCO}\)

\( \Rightarrow \widehat {CAO} + \widehat {COA} = \widehat {ACM}{\rm{ }} + \widehat {MCO}{\rm{ }} = \widehat {ACO}{\rm{ }}\left( 3 \right)\)

Mặt khác ta lại có: \(\widehat {CAO} + \widehat {COA} + \widehat {ACO} = {180^o}\,\,\,\,\left( 4 \right)\) (tổng 3 góc trong tam giác)

Từ (3) và (4) \( \Rightarrow \widehat {ACO} =180^0:2= {90^o}\)

Suy ra \(AC\bot CO\) tại \(C\), mà \(C\in (O)\)

Do đó AC là tiếp tuyến của (O)

Loigiaihay.com


Bình chọn:
4.3 trên 27 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store