 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Đề kiểm tra 15 phút - Đề số 3 - Bài 5 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 5 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn tâm O, đường kính AB. Kẻ tiếp tuyến tại B với đường tròn (O), trên tiếp tuyến lấy P. Qua A kẻ đường thẳng song song với OP cắt (O) tại Q. Chứng minh PQ là tiếp tuyến của đường tròn (O).
Phương pháp giải - Xem chi tiết
-Dựa vào tính chất của hai đường thẳng song song chỉ ra góc QOP bằng góc BOP
-Từ đó chứng minh được tam giác OPQ bằng tam giác OPB
=>PQ vuông góc với OQ
Lời giải chi tiết
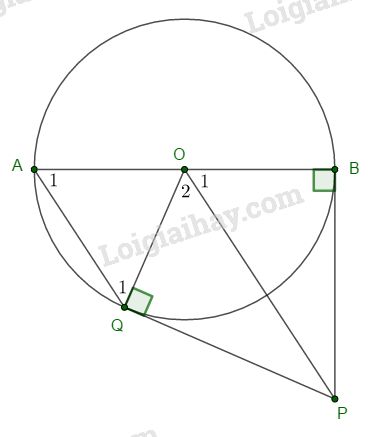
Ta có: AQ // OP (gt)
\(\left\{ {\matrix{ {{{\widehat A}_1} = {{\widehat O}_1}\,\left( \text{cặp góc đồng vị} \right)} \cr {{{\widehat Q}_1} = {{\widehat O}_2}\,\left( \text{cặp góc so le trong} \right)} \cr } } \right.\)
mà \({\widehat A_1} = {\widehat Q_1}\) (∆AOQ cân) \( \Rightarrow {\widehat O_1} = {\widehat O_2}\)
Xét \(∆PQO\) và \(∆PBO\) có:
OP chung
\({\widehat O_1} = {\widehat O_2}\) (cmt)
\(OQ = OB (=R)\)
Vậy \(∆PQO = ∆PBO\) (c.g.c) \( \Rightarrow \widehat {PQO} = \widehat {PBO} = 90^o\)
Hay \(PQ ⊥ OQ\), chứng tỏ PQ là tiếp tuyến của (O).
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận