 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Hình học 9
Đề bài
Cho tam giác ABC, các đường cao AD, BE và CF. Gọi H là trực tâm của tam giác.
a. Chứng minh bốn điểm A, E, H, F cùng nằm trên một đường tròn xác định tâm I
b. Gọi O là trung điểm của BC. Chứng minh OE là tiếp tuyến của đường tròn (I).
Phương pháp giải - Xem chi tiết
a. Chứng minh tứ giác AEHF có tổng 2 góc đối bằng 180 độ
b. Sử dụng:
+Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh cạnh huyền
+Hai góc cùng phụ với góc thứ ba thì bằng nhau
Lời giải chi tiết
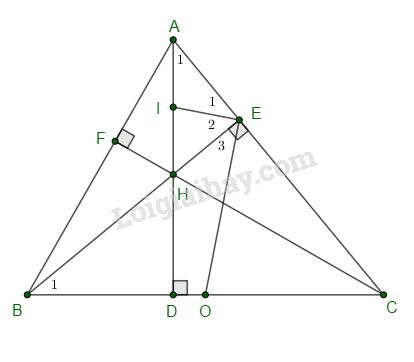
a. Ta có: \(\widehat {AFH} = \widehat {AEH} = 90^\circ \) (gt)
⇒ E, F nằm trên đường tròn đường kính AH có tâm I là trung điểm đoạn AH.
b. ∆BEC vuông tại E có O là trung điểm của BC (gt)
\( \Rightarrow OE = OB = {{BC} \over 2}\) nên \({\widehat E_3} = {\widehat B_1};{\widehat B_1} = {\widehat A_1}\) (cùng phụ với góc C)
∆AIE cân \( \Rightarrow {\widehat A_1} = {\widehat E_1}.\) Do đó \({\widehat E_3} = {\widehat E_1},\) mà \({\widehat E_1} + {\widehat E_2} = 90^\circ \) (gt)
\( \Rightarrow {\widehat E_3} + {\widehat E_2} = 90^\circ \) hay OE là tiếp tuyến của (I)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận