Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Bài 24 trang 111 SGK Toán 9 tập 1


Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB,...

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho đường tròn \((O)\), dây \(AB\) khác đường kính. Qua \(O\) kẻ đường vuông góc với \(AB\), cắt tiếp tuyến tại \(A\) của đường tròn ở điểm \(C\). 

a) Chứng minh rằng \(CB\) là tiếp tuyến của đường tròn.

b) Cho bán kính của đường tròn bằng \(15cm,\ AB=24cm\). Tính độ dài \(OC\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Dùng dấu hiệu nhận biết tiếp tuyến: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Sử dụng tính chất:

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm đó.

b) Sử dụng định lí Pytago: \(\Delta ABC\) vuông tại \(A\), khi đó: \(BC^2=AC^2+AB^2\).

Sử dụng hệ thức lượng trong tam giác vuông: \(\Delta ABC\), vuông tại \(A\), \(AH \bot BC\), khi đó: \(AB^2=BH.BC\). 

Lời giải chi tiết

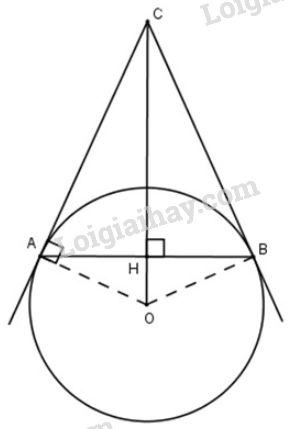
a) Gọi \(H\) là giao điểm của \(OC\) và \(AB\).

Xét đường tròn (O) có \(OH\perp AB\) tại H mà OH là 1 phần đường kính và AB là dây của đường tròn nên \(HA=HB=\dfrac{AB}2\) (Định lý 2 - trang 103).

Suy ra \(OC\) là đường trung trực của \(AB\), do đó \(CB=CA\) (tính chất)

Xét \(\Delta CBO\) và \(\Delta CAO\) có:

\(CO\) chung 

\(CA=CB\) (chứng minh trên) 

\(OB=OA=R\)

Suy ra \(\Delta CBO=\Delta CAO\) (c.c.c)

\(\Rightarrow \widehat{CBO}=\widehat{CAO}\)( 2 góc tương ứng)  (1)

Vì \(AC\) là tiếp tuyến của đường tròn \((O)\) nên:

\(AC\perp OA\Rightarrow \widehat{CAO}=90^{\circ}\)   (2)

Từ (1) và (2) suy ra \(\widehat{CBO}=90^{\circ}\).

Tức là \(CB\) vuông góc với \(OB\), mà \(OB\) là bán kính của \((O)\).

Vậy \(CB\) là tiếp tuyến của đường tròn \((O)\).

b) Ta có: \(OA=OB=R=15 cm;\)

\(\ HA=\dfrac{AB}{2}=\dfrac{24}{2}=12 cm\).

Xét tam giác \(HOA\) vuông tại \(H\), áp dụng định lí Pytago, ta có: 

\(OA^2=OH^2+AH^2\)

\(\Leftrightarrow OH^{2}=OA^{2}-AH^{2}=15^{2}-12^{2}=81\)

\(\Rightarrow OH=\sqrt{81}=9(cm)\)

Xét tam giác \(BOC\) vuông tại \(B\), áp dụng hệ thức lượng trong tam giác vuông, ta có:

\(OB^{2}=OC\cdot OH \Rightarrow OC=\dfrac{OB^{2}}{OH}=\dfrac{15^2}{9}=25(cm).\)


Bình chọn:
4.5 trên 146 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store