Đề số 4 – Đề kiểm tra học kì 2 – Toán 8

Đề bài

I. TRẮC NGHIỆM (2 điểm)

Chọn chữ cái đứng trước câu trả lời đúng

Câu 1: Tập nghiệm của phương trình $\left( {{x^2} + 25} \right)\left( {{x^2} - \dfrac{9}{4}} \right) = 0$ là:

A. $\left\{ { \pm 5; \pm \dfrac{3}{2}} \right\}$                        B. $\left\{ { - 25;\dfrac{9}{4}} \right\}$

C. $\left\{ { \pm \dfrac{3}{2}} \right\}$                       D. $\left\{ { - 5;\dfrac{3}{2}} \right\}$

Câu 2:   Nghiệm của bất phương trình: $12 - 3x \le 0$ là:

A. $x \le 4$                B. $x \ge 4$ 

C. $x \le  - 4$              D. $x \ge  - 4$

Câu 3:  Cho tam giác $ABC$ đồng dạng với tam giác $MNP$ và $\dfrac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9$  

A. $\dfrac{{MN}}{{AB}} = 9$               B. $\dfrac{{MN}}{{AB}} = 3$

C. $\dfrac{{MN}}{{AB}} = \dfrac{1}{9}$                       D. $\dfrac{{MN}}{{AB}} = \dfrac{1}{3}$ 

Câu 4:  Cho tam giác $ABC,\,\,AD$ là  phân giác của $\angle BAC$, biết $AB = 16cm,\,\,AC = 24cm,\,\,DC = 15cm$. Khi đó $BD$ bằng:

A. $10cm$                  B. $\dfrac{{128}}{5}cm$

C. $\dfrac{1}{{10}}cm$                       D. $\dfrac{{45}}{2}cm$ 

II. TỰ LUẬN:

Bài 1 (2,5 điểm):

Cho hai biểu thức $A = \dfrac{1}{{y - 1}} - \dfrac{y}{{1 - {y^2}}}$ và $B = \dfrac{{{y^2} - y}}{{2y + 1}}$

1. Tính giá trị biểu thức $A$ tại $y = 2$.

2. Rút gọn biểu thức $M = A.B$.

3. Tìm giá trị của $y$ để biểu thức $M < 1$.

Bài 2 (2 điểm):

Một ô tô đi từ Hà Nội đến Đền Hùng với vận tốc trung bình là $30km/h$ . Trên quãng đường từ Đền Hùng về Hà Nội, vận tốc ô tô tăng thêm $10km/h$ nên thời gian về rút ngắn hơn thời gian đi là $36$ phút. Tính quãng đường từ Hà Nội đến Đền Hùng.

Bài 3 (3 điểm):

Cho tam giác $ABC$ vuông tại $B$, đường cao $BH$.

a. CMR: $\Delta HBA$ đồng dạng với $\Delta HCB$, từ đó suy ra $H{B^2} = HC.HA$.

b. Kẻ $HM \bot AB = \left\{ M \right\},\,$$HN \bot BC = \left\{ N \right\}$. CMR: $MN = BH$.

c. Lấy $I,\,\,K$ lần lượt là trung điểm của $HC$ và $HA$. Tứ giác $KMNI$ là hình gì? Vì sao?

d. So sánh diện tích tứ giác $KMNI$ và diện tích tam giác $ABC$.

Bài 4  (0,5 điểm):

Cho $a,b,c > 0$. Chứng minh: $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}} \ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$

Đ/a TN

Câu 1:

Phương pháp:

Áp dụng các tính chất và cách giải phương trình tích:    $A\left( x \right).B\left( x \right) = 0$ $\Rightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.$

Cách giải:

$\begin{array}{l}\left( {{x^2} + 25} \right)\left( {{x^2} - \dfrac{9}{4}} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}{x^2} + 25 = 0\\{x^2} - \dfrac{9}{4} = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{x^2} =  - 25\,\,\,\,\left( {ktm} \right)\\{x^2} = \dfrac{9}{4}\,\,\,\,\,\,\,\,\,\,\, \Rightarrow x =  \pm \dfrac{3}{2}\end{array} \right.\end{array}$

Vậy tập nghiệm của phương trình $\left( {{x^2} + 25} \right)\left( {{x^2} - \dfrac{9}{4}} \right) = 0$ là $S = \left\{ { \pm \dfrac{3}{2}} \right\}.$

Chọn C.

Câu 2:

Phương pháp:

Giải bất phương trình bậc nhất một ẩn bằng các quy tắc chuyển vế đổi dấu và chia cả hai vế của bất phương trình cho cùng một số âm thì đổi dấu của bất phương trình.

Cách giải:

$12 - 3x \le 0 \Leftrightarrow  - 3x \le  - 12$ $\Leftrightarrow x \ge 4$

Vậy nghiệm của bất phương trình: $12 - 3x \le 0$ là $x \ge 4$

Chọn B.

Câu 3:

Phương pháp:

Hai tam giác đồng dạng theo tỉ số đồng dạng là $k$ thì tỉ số của diện tích hai tam giác đó là ${k^2}.$

Cách giải:

Do $\Delta ABC \backsim \Delta MNP$  nên  $\dfrac{{{S_{ABC}}}}{{{S_{MNP}}}} = {\left( {\dfrac{{AB}}{{MN}}} \right)^2}$ 

Mà $\dfrac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9$  nên  suy ra ${\left( {\dfrac{{AB}}{{MN}}} \right)^2} = 9$$\Rightarrow \dfrac{{AB}}{{MN}} = 3 \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{1}{3}$

Vậy  $\dfrac{{MN}}{{AB}} = \dfrac{1}{3}$  

Chọn D.

Câu 4:

Phương pháp:

Áp dụng tính chất của tia phân giác: Cho $\Delta ABC$ có đường phân giác $AD$ ta có tỉ lệ: $\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}}.$

Cách giải:

Vì $\,AD$ là  phân giác của $\angle BAC$, áp dụng tính chất tia phân giác ta có:

$\begin{array}{l}\dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\\ \Rightarrow \dfrac{{16}}{{24}} = \dfrac{{DB}}{{15}}\\ \Rightarrow DB = \dfrac{{16.15}}{{24}} = 10\,\,(cm)\end{array}$

Vậy $DB = 10cm$

Chọn A. 

LG bài 1

Phương pháp giải:

1. Thay $y = 2$ vào biểu thức $A$ rồi tính giá trị biểu thức đó.

2. Rút gọn biểu thức $A$ sau đó thức hiện phép nhân hai biểu thức $A$ và $B$.

3. Dựa vào kết quả ở câu 2 để lập luận tìm giá trị của $y$ sao cho $M < 1$.

Lời giải chi tiết:

1. Tính giá trị của biểu thức A  tại $y = 2.$

Điều kiện: $y \ne  \pm 1.$

Thay $y = 2\,\,\,\left( {tm} \right)$  vào biểu thức $A$ ta được

$\begin{array}{l}A = \dfrac{1}{{2 - 1}} - \dfrac{2}{{1 - {2^2}}}\\ = \dfrac{1}{1} - \dfrac{2}{{1 - 4}} = 1 - \dfrac{2}{{ - 3}}\\ = 1 + \dfrac{2}{3} = \dfrac{5}{3}\end{array}$

Vậy với  $y = 2\,\,$thì $A = \dfrac{5}{3}.$

2. Rút gọn biểu thức $M = A.B.$

ĐKXĐ:  $y \ne  \pm 1\,;\,\,y \ne \dfrac{1}{2}$.

Ta có:

$\begin{array}{l}A = \dfrac{1}{{y - 1}} - \dfrac{y}{{1 - {y^2}}} = \dfrac{1}{{y - 1}} + \dfrac{y}{{{y^2} - 1}}\\ = \dfrac{{y + 1}}{{(y - 1)(y + 1)}} + \dfrac{y}{{(y - 1)(y + 1)}}\\ = \dfrac{{y + 1 + y}}{{(y - 1)(y + 1)}} = \dfrac{{2y + 1}}{{(y - 1)(y + 1)}}.\\ \Rightarrow M = A.B\\ = \dfrac{{2y + 1}}{{(y - 1)(y + 1)}} \cdot \dfrac{{{y^2} - y}}{{2y + 1}}\\ = \dfrac{{2y + 1}}{{(y - 1)(y + 1)}} \cdot \dfrac{{y(y - 1)}}{{2y + 1}}\\ = \dfrac{y}{{y + 1}}.\end{array}$

3. Tìm giá trị của y  để $M < 1.$

Điều kiện: $y \ne  \pm 1\,;\,\,y \ne \dfrac{1}{2}$

$\begin{array}{l}M < 1 \Leftrightarrow \dfrac{y}{{y + 1}} < 1\\ \Leftrightarrow \dfrac{y}{{y + 1}} - 1 < 0\\ \Leftrightarrow \dfrac{y}{{y + 1}} - \dfrac{{y + 1}}{{y + 1}} < 0\\ \Leftrightarrow \dfrac{{y - (y + 1)}}{{y + 1}} < 0\\ \Leftrightarrow \dfrac{{ - 1}}{{y + 1}} < 0\end{array}$

Vì  $- 1 < 0$  nên  $\dfrac{{ - 1}}{{y + 1}} < 0$$\Rightarrow y + 1 > 0 \Rightarrow y >  - 1$

Vậy để biểu thức $M < 1$ thì $y >  - 1;\,\,y \ne 1;\,\,y \ne \dfrac{1}{2}$.

LG bài 2

Phương pháp giải:

Bước 1. Lập phương trình:

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Lời giải chi tiết:

Gọi quãng đường từ Hà Nội đến Đền Hùng là $x\;\left( {km} \right),\;\;\left( {x > 0} \right).$

Vận tốc của ô tô  khi đi từ Đền Hùng về Hà Nội là:  $30 + 10 = 40\,\,(km/h)$

Thời gian ô tô đi từ Hà Nội đến Đền Hùng là $\dfrac{x}{{30}}\;\;\left( h \right).$

Thời gian ô tô đi từ Đền Hùng về Hà Nội là $\dfrac{x}{{40}}\;\;\left( h \right).$

Đổi: $36$  phút $= \dfrac{3}{5}\;\;\left( h \right).$

Vì thời gian về rút ngắn hơn thời gian đi là $36$ phút nên ta có phương trình:

$\begin{array}{l}\dfrac{x}{{30}} - \dfrac{x}{{40}} = \dfrac{3}{5}\\ \Leftrightarrow \dfrac{{4x}}{{120}} - \dfrac{{3x}}{{120}} = \dfrac{{72}}{{120}}\\ \Rightarrow 4x - 3x = 72\\ \Leftrightarrow x = 72\;\;\left( {tm} \right)\end{array}$

Vậy quãng đường đi từ Hà Nội đến đền Hùng là 72 km.

LG bài 3

Phương pháp giải:

a) Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc.

b) Chứng minh tứ giác $HMAN$ là hình chữ nhật, từ đó suy ra $MN = BH$.

Lời giải chi tiết:

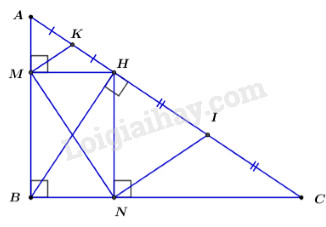
a. Xét $\Delta HBA$ và $\Delta HCB$ ta có:

$\angle HBA = \angle HCB$ (cùng phụ với $\angle BAC$)

$\angle AHB = \angle BHC = {90^0}$

$\Rightarrow \Delta HBA \backsim \Delta HCB\,\,\,\left( {g - g} \right)$

$\begin{array}{l} \Rightarrow \dfrac{{HB}}{{HC}} = \dfrac{{HA}}{{HB}}\\ \Rightarrow H{B^2} = HC.HA\,\,\end{array}$

b. Ta có $HM \bot AB = \left\{ M \right\},\,\,$$HN \bot BC = \left\{ N \right\}$ nên $\angle HMB = \angle HNB = {90^0}$.

Lại có $\angle MBN = {90^0}$ (vì tam giác $ABC$ vuông tại $B$)

Tứ giác $HMAN$ có 3 góc vuông nên đó là hình chữ nhật, suy ra $MN = BH$ (hai đường chéo của hình chữ nhật).

c. $MH//BC$ nên $\angle KHM = \angle ICN$ (hai góc đồng vị)

$K$ là trung điểm cạnh huyền $AH \Rightarrow KH = KA = KM$ $\Rightarrow \Delta KHM$ cân tại $K \Rightarrow \angle KHM = \angle KMH\,\,\left( {tc} \right)$ 

$I$ là trung điểm cạnh huyền $HC \Rightarrow IN = IH = IC$$\Rightarrow \Delta IHC$ cân tại $I \Rightarrow \angle ICN = \angle INC\,\,\,\left( {tc} \right).$

$\angle HIN = \angle INC + \angle ICN$ (góc ngoài tam giác)

$\angle MKH + \angle HIN$ $= \angle MKH + 2\angle ICN$$= \angle MKH + 2\angle KHM = {180^0}$

Nên $MK//NI$, suy ra $KMNI$ là hình thang (dhnb).

Xét $\Delta KAM$ có $KA = KM\left( { = \dfrac{1}{2}AH} \right)$  nên $\Delta KAM$ là tam giác cân, suy ra $\angle KAM = \angle AMK$.

Vì $HMBN$ là hình chữ nhật nên $\angle NMB = \angle MBH$ (tính chất hình chữ nhật)

Mà $\angle MBH = \angle BCA\,\,$$\Rightarrow \angle AMK + \angle NMB$$= \angle MAH + \angle ICN = {90^0}$

Suy ra $KMNI$ là hình thang vuông tại $M,\,\,N.$

d. Ta có:

$\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}AC.BH\\{S_{KMNI}} = \dfrac{1}{2}(KM + NI).MN\\ = \dfrac{1}{2}.\left( {\dfrac{1}{2}AH + \dfrac{1}{2}HC} \right).BH\\ = \dfrac{1}{4}AC.BH\\ \Rightarrow {S_{KMNI}} = \dfrac{1}{2}{S_{ABC}}\end{array}$

LG bài 4

Phương pháp giải:

Cách 1: Chứng minh $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}} \ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$ bằng cách chứng minh $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}} - \dfrac{1}{a} - \dfrac{1}{b} - \dfrac{1}{c} \ge 0$

Cách 2: Sử dụng bất đẳng thức Cauchy.

Lời giải chi tiết:

Cách 1:

Ta có: $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}} \ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$$\Leftrightarrow \dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}}$$- \dfrac{1}{a} - \dfrac{1}{b} - \dfrac{1}{c} \ge 0$

$\Leftrightarrow \dfrac{a}{{{b^2}}} - \dfrac{2}{b} + \dfrac{1}{a} + \dfrac{b}{{{c^2}}} - \dfrac{2}{c}$$+ \dfrac{1}{b} + \dfrac{c}{{{a^2}}} - \dfrac{2}{a} + \dfrac{1}{c} \ge 0$

$\Leftrightarrow {\left( {\dfrac{{\sqrt a }}{b}} \right)^2} - 2.\dfrac{{\sqrt a }}{b}.\dfrac{1}{{\sqrt a }} + {\left( {\dfrac{1}{{\sqrt a }}} \right)^2}$$+ {\left( {\dfrac{{\sqrt b }}{c}} \right)^2} - 2.\dfrac{{\sqrt b }}{c}.\dfrac{1}{{\sqrt b }} + {\left( {\dfrac{1}{{\sqrt b }}} \right)^2}$$+ {\left( {\dfrac{{\sqrt c }}{a}} \right)^2} - 2.\dfrac{{\sqrt c }}{a}.\dfrac{1}{{\sqrt c }} + {\left( {\dfrac{1}{{\sqrt c }}} \right)^2} \ge 0$

$\Leftrightarrow {\left( {\dfrac{{\sqrt a }}{b} - \dfrac{1}{{\sqrt a }}} \right)^2} + {\left( {\dfrac{{\sqrt b }}{c} - \dfrac{1}{{\sqrt b }}} \right)^2}$ $+ {\left( {\dfrac{{\sqrt c }}{a} - \dfrac{1}{{\sqrt c }}} \right)^2} \ge 0$(đúng với mọi $a,b,c > 0$)

Dấu  xảy ra khi $a = b = c$

Vậy với $a,\,b,\,c > 0$  thì $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}}$ $\ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}.$

Cách 2:

Với $a,b,c > 0$, áp dụng BĐT Cô-si ta được:

$\begin{array}{l}\dfrac{a}{{{b^2}}} + \dfrac{1}{a} \ge 2\sqrt {\dfrac{a}{{{b^2}}}.\dfrac{1}{a}}  \ge \dfrac{2}{b}\,\,;\\\dfrac{b}{{{c^2}}} + \dfrac{1}{b} \ge 2\sqrt {\dfrac{b}{{{c^2}}}.\dfrac{1}{b}}  \ge \dfrac{2}{c}\,\,;\\\dfrac{c}{{{a^2}}} + \dfrac{1}{c} \ge 2\sqrt {\dfrac{c}{{{a^2}}}.\dfrac{1}{c}}  \ge \dfrac{2}{a}\,.\end{array}$

Cộng vế với vế các BĐT trên ta được:

$\dfrac{a}{{{b^2}}} + \dfrac{1}{a} + \dfrac{b}{{{c^2}}} + \dfrac{1}{b} + \dfrac{c}{{{a^2}}} + \dfrac{1}{c}$$\ge \dfrac{2}{b} + \dfrac{2}{c} + \dfrac{2}{a}$

$\Leftrightarrow \dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}}$$\ge \dfrac{2}{b} + \dfrac{2}{c} + \dfrac{2}{a} - \dfrac{1}{a} - \dfrac{1}{b} - \dfrac{1}{c}$

$\Leftrightarrow \dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}}$$\ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$ (đpcm)

Vậy với $a,b,c > 0$ thì $\dfrac{a}{{{b^2}}} + \dfrac{b}{{{c^2}}} + \dfrac{c}{{{a^2}}}$$\ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$. Dấu  xảy ra khi $a = b = c$.

Nguồn sưu tầm

Loigiaihay.com