Đề kiểm tra giữa kì II Toán 8 - Đề số 4 có lời giải chi tiết
Đề kiểm tra giữa kì 2 toán 8 - Đề số 4 có lời giải chi tiết
Đề bài
Câu 1 (2 điểm): Giải phương trình:
a) \(\left( {3x - 2} \right)\left( {2x + 1} \right) = {\left( {2x + 1} \right)^2}\)
b) \(\frac{2}{{x - 2}} - \frac{3}{{3 - x}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\)
Câu 2 (2 điểm): Giải bài toán bằng cách lập phương trình:
Một miếng đất hình chữ nhật có chiều rộng bé hơn chiều dài \(25m\). Nếu giảm chiều dài \(25m\) thì diện tích mảnh đất sẽ nhỏ hơn diện tích ban đầu là \(1000{m^2}\). Tính các kích thước của miếng đất ban đầu.
Câu 3 (2 điểm): Cho phương trình \(\left( {{m^2} + 2m + 3} \right)x - 6 = 0\) (\(m\) là tham số)
a) Tính giá trị của \(m\) để phương trình nhận \(x = 2\) là một nghiệm.
b) Tìm giá trị của \(m\) để phương trình có nghiệm \(x\) duy nhất đạt giá trị lớn nhất.
Câu 4 (3,5 điểm): Cho \(\Delta ABC\) vuông tại \(A,\,\,AB < AC,\,\,AH\) là đường cao.
a) Chứng minh \(\Delta HAC\) và \(\Delta ABC\) đồng dạng.
b) Chứng minh \(H{A^2} = HB.HC\)
c) Gọi \(D,\,\,E\) lần lượt là trung điểm của \(AB,\,\,BC\). Chứng minh \(CH.CB = 4D{E^2}\).
d) Gọi \(M\) là giao điểm của đường thẳng vuông góc với \(BC\) tại \(B\) và đường thẳng \(DE\). Gọi \(N\) là giao điểm của \(AH\) và \(CM\). Chứng minh \(N\) là trung điểm của \(AH\).
Câu 5 (0,5 điểm): Cho ba số \(a,\,\,b,\,\,c\) thỏa mãn \(0 < a \le b \le c\). Chứng minh rằng:
\(\frac{a}{b} + \frac{b}{c} + \frac{c}{a} \ge \frac{b}{a} + \frac{c}{b} + \frac{a}{c}\)
Lời giải chi tiết
Câu 1 (VD)
Phương pháp:
a) Đưa phương trình đã cho về dạng phương trình tích:
\(A\left( x \right).B\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
b) Phương trình chứa ẩn ở mẫu:
+ Tìm điều kiện xác định của phương trình.
+ Quy đồng hai vế của phương trình rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Kết luận.
Cách giải:
a) \(\left( {3x - 2} \right)\left( {2x + 1} \right) = {\left( {2x + 1} \right)^2}\)
\(\begin{array}{l}\left( {3x - 2} \right)\left( {2x + 1} \right) = {\left( {2x + 1} \right)^2}\\ \Leftrightarrow \left( {3x - 2} \right)\left( {2x + 1} \right) - {\left( {2x + 1} \right)^2} = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left[ {\left( {3x - 2} \right) - \left( {2x + 1} \right)} \right] = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left( {3x - 2 - 2x - 1} \right) = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - \frac{1}{2};\,\,3} \right\}\).
b) \(\frac{2}{{x - 2}} - \frac{3}{{3 - x}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\)
Điều kiện: \(\left\{ \begin{array}{l}x - 2 \ne 0\\3 - x \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne 3\end{array} \right.\)
\(\frac{2}{{x - 2}} - \frac{3}{{3 - x}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\)
\( \Leftrightarrow \frac{2}{{x - 2}} + \frac{3}{{x - 3}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\)
\(\begin{array}{l} \Leftrightarrow \frac{{2\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x - 2} \right)}} + \frac{{3\left( {x - 2} \right)}}{{\left( {x - 3} \right)\left( {x - 2} \right)}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\\ \Rightarrow 2\left( {x - 3} \right) + 3\left( {x - 2} \right) = 3x - 20\\ \Leftrightarrow 2x - 6 + 3x - 6 = 3x - 20\\ \Leftrightarrow 2x - 6 + 3x - 6 - 3x + 20 = 0\\ \Leftrightarrow 2x + 8 = 0\\ \Leftrightarrow 2x = - 8\\ \Leftrightarrow x = - 4\,\,\left( {tm} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 4} \right\}\).
Câu 2 (VD)
Phương pháp:
Các bước giải bài toán bằng cách lập phương trình:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Kết hợp với điều kiện xác định và kết luận.
Cách giải:
Giải bài toán bằng cách lập phương trình.
Gọi chiều rộng của miếng đất ban đầu là \(x\,\,\left( {m,\,\,x > 0} \right)\).
Chiều dài của miếng đất ban đầu là \(x + 25\,\,\left( m \right)\).
Diện tích của miếng đất ban đầu là \(x\left( {x + 25} \right)\,\,\left( {{m^2}} \right)\).
Chiều dài của miếng đất sau khi giảm đi \(25m\) là \(\left( {x + 25} \right) - 25 = x\,\,\left( m \right)\).
Diện tích của miếng đất sau khi giảm chiều dài là \({x^2}\,\,\left( {{m^2}} \right)\).
Vì giảm chiều dài \(25m\) thì diện tích mảnh đất sẽ nhỏ hơn diện tích ban đầu là \(1000{m^2}\) nên ta có phương trình:
\(\begin{array}{l}x\left( {x + 25} \right) - {x^2} = 1000\\ \Leftrightarrow {x^2} + 25x - {x^2} = 1000\\ \Leftrightarrow 25x = 1000\\ \Leftrightarrow x = 40\,\,\left( {tm} \right)\end{array}\)
Chiều rộng của miếng đất ban đầu là \(40m\).
Vậy chiều dài của miếng đất ban đầu là \(40 + 25 = 65\left( m \right)\).
Câu 3 (VD)
Phương pháp:
a) Thay giá trị \(x = 2\) vào phương trình đã cho để tìm \(m\).
b) Chứng minh phương trình có nghiệm duy nhất với mọi \(m\). Đưa phương trình về dạng \(ax + b = 0\)\( \Leftrightarrow x = - \frac{b}{a}\).
Từ đó tìm giá trị lớn nhất của \(x\).
Cách giải:
Cho phương trình \(\left( {{m^2} + 2m + 3} \right)x - 6 = 0\) (\(m\) là tham số)
a) Tính giá trị của \(m\) để phương trình nhận \(x = 2\) là một nghiệm.
Vì \(x = 2\) là nghiệm của phương trình \(\left( {{m^2} + 2m + 3} \right)x - 6 = 0\) nên ta có:
\(\begin{array}{l}\left( {{m^2} + 2m + 3} \right).2 - 6 = 0\\ \Leftrightarrow 2{m^2} + 4m + 6 - 6 = 0\\ \Leftrightarrow 2{m^2} + 4m = 0\\ \Leftrightarrow 2m\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\end{array}\)
Vậy \(m \in \left\{ { - 2;\,\,0} \right\}\).
b) Tìm giá trị của \(m\) để phương trình có nghiệm \(x\) duy nhất đạt giá trị lớn nhất.
Phương trình \(\left( {{m^2} + 2m + 3} \right)x - 6 = 0\) có nghiệm duy nhất khi và chỉ khi
\({m^2} + 2m + 3 \ne 0\)\( \Leftrightarrow {m^2} + 2m + 1 + 2 \ne 0\)\( \Leftrightarrow {\left( {m + 1} \right)^2} + 2 \ne 0\)với mọi \(m\).
Suy ra, với mọi giá trị của \(m\) thì phương trình có nghiệm duy nhất.
Ta có:
\(\begin{array}{l}\left( {{m^2} + 2m + 3} \right)x - 6 = 0\\ \Leftrightarrow \left( {{m^2} + 2m + 3} \right)x = 6\\ \Leftrightarrow x = \frac{6}{{{m^2} + 2m + 3}}\\ \Leftrightarrow x = \frac{6}{{{{\left( {m + 1} \right)}^2} + 2}}\end{array}\)
Vì \({\left( {m + 1} \right)^2} \ge 0\) với mọi \(m\)
\( \Rightarrow {\left( {m + 1} \right)^2} + 2 \ge 2\) với mọi \(m\)
\( \Rightarrow \frac{6}{{{{\left( {m + 1} \right)}^2} + 2}} \le \frac{6}{2}\) với mọi \(m\)
\( \Rightarrow x \le 3\) với mọi \(m\)
Dấu “\( = \)” xảy ra khi và chỉ khi \(m + 1 = 0 \Leftrightarrow m = - 1\) (thỏa mãn)
Do đó, \(x\) đạt giá trị lớn nhất bằng \(3\) khi \(m = - 1\).
Vậy \(m = - 1\) thì phương trình có nghiệm \(x\) duy nhất đạt giá trị lớn nhất.
Câu 4 (VD)
Phương pháp:
a) Chứng minh tam giác đồng dạng theo trường hợp góc – góc.
b) Chứng minh tam giác đồng dạng để có tỉ số \(\frac{{BH}}{{AH}} = \frac{{AH}}{{CH}}\). Từ đó, chứng minh được \(A{H^2} = BH.CH\).
c) Áp dụng câu b \(\left( {A{H^2} = BH.CH} \right)\) và áp dụng định nghĩa đường trung bình trong \(\Delta ABC\).
d) Chứng minh \(HN = AN\) từ \(\frac{{HN}}{{BM}} = \frac{{AN}}{{PM}}\) (áp dụng hệ quả của định lý Ta-lét)
Hệ quả của định lý Ta-lét:
\(a\,{\rm{//}}\,BC\)\( \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{BC'}}{{BC}}\)
Cách giải:
Cho \(\Delta ABC\) vuông tại \(A,\,\,AB < AC,\,\,AH\) là đường cao.
a) Chứng minh \(\Delta HAC\) và \(\Delta ABC\) đồng dạng.
Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\angle BAC = \angle AHC\,\,\left( { = {{90}^ \circ }} \right)\)
\(\angle C\) chung
\( \Rightarrow \Delta ABC \sim \Delta HAC\) (góc-góc)
b) Chứng minh \(H{A^2} = HB.HC\).
\(\Delta ABH\) vuông tại \(H\)\( \Rightarrow \angle BAH + \angle HBA = {90^0}\) (tổng ba góc trong tam giác)
\(\Delta ABC\) vuông tại \(A\)\( \Rightarrow \angle BAH + \angle CAH = {90^0}\) (tổng ba góc trong tam giác)
\( \Rightarrow \angle HBA = \angle CAH\) (vì cùng phụ với \(\angle BAH\))
Xét \(\Delta BAH\) và \(\Delta ACH\) có:
\(\angle AHB = \angle CHA\,\,\left( { = {{90}^0}} \right)\)
\(\angle BAH = \angle ACH\) (chứng minh trên)
\( \Rightarrow \Delta BAH \sim \Delta ACH\) (góc-góc)
\( \Rightarrow \frac{{BH}}{{AH}} = \frac{{AH}}{{CH}}\)(tỷ số cặp cạnh tương ứng)
\( \Rightarrow A{H^2} = BH.CH\)(đpcm)
c) Gọi \(D,\,\,E\) lần lượt là trung điểm của \(AB,\,\,BC\). Chứng minh \(CH.CB = 4D{E^2}\).
Theo câu a) ta có: \(\Delta ABC \sim \Delta HAC\)
\( \Rightarrow \frac{{BC}}{{AC}} = \frac{{AC}}{{HC}}\) (tỷ số cặp cạnh tương ứng)
\( \Rightarrow A{C^2} = HC.BC\) \(\left( 1 \right)\)
Xét \(\Delta ABC\) ta có:
\(D\) là trung điểm của \(AB\) (giả thiết)
\(E\) là trung điểm của \(BC\) (giả thiết)
\( \Rightarrow DE\) là đường trung bình của \(\Delta ABC\) (định nghĩa đường trung bình trong tam giác)
\( \Rightarrow DE = \frac{1}{2}AC\) (tính chất)
\( \Leftrightarrow AC = 2DE\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\) suy ra: \({\left( {2DE} \right)^2} = HC.BC\)
\( \Leftrightarrow 4D{E^2} = HC.BC\) hay \(CH.CB = 4D{E^2}\)(đpcm).
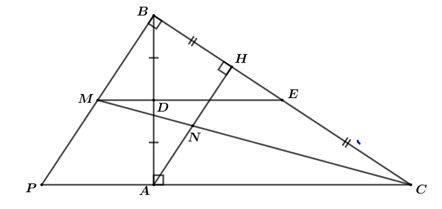
d) Gọi \(M\) là giao điểm của đường thẳng vuông góc với \(BC\) tại \(B\) và đường thẳng \(DE\). Gọi \(N\) là giao điểm của \(AH\) và \(CM\). Chứng minh \(N\) là trung điểm của \(AH\).
Gọi \(P\) là giao điểm của \(MB\) và \(AC\).
Vì \(DE\) là đường trung bình của \(\Delta ABC\) nên \(DE\,{\rm{//}}\,AC\) (tính chất đường trung bình)\( \Rightarrow ME\,{\rm{//}}\,AC\).
Xét \(\Delta BPC\) có :\(ME\,{\rm{//}}\,AC\) và \(E\) là trung điểm của \(BC\).
\( \Rightarrow \) \(M\) là trung điểm của \(BP\) (định lí đường trung bình trong tam giác)
\( \Rightarrow BM = PM\)
Ta có:
\(AH \bot BC\) tại \(H\)
\(PB \bot BC\) tại \(B\)
\( \Rightarrow AH\,{\rm{//}}\,{\rm{BP}}\) (quan hệ từ vuông góc đến song song)
\( \Rightarrow HN\,{\rm{//}}\,BM,\,AN\,{\rm{//}}\,PM\) (vì \(N \in AH,\,\,M \in BP\))
Xét \(\Delta BCM\) có \(HN\,{\rm{//}}\,BM\), áp dụng hệ quả của định lý Ta-let ta có: \(\frac{{CN}}{{CM}} = \frac{{HN}}{{BM}}\)
Xét \(\Delta PCM\) có \(AN\,{\rm{//}}\,PM\), áp dụng hệ quả của định lý Ta-let ta có: \(\frac{{AN}}{{PM}} = \frac{{CN}}{{CM}}\)
\( \Rightarrow \frac{{HN}}{{BM}} = \frac{{AN}}{{PM}}\)\(\left( { = \frac{{CN}}{{CM}}} \right)\)
Mà \(PM = BM\) (vì \(M\) là trung điểm của \(BP\))
\( \Rightarrow HN = AN\)
\( \Rightarrow \) \(N\) là trung điểm của \(AH\).
Câu 5 (VDC)
Phương pháp:
Chứng minh hiệu \(\left( {\frac{a}{b} + \frac{b}{c} + \frac{c}{a}} \right) - \left( {\frac{b}{a} + \frac{c}{b} + \frac{a}{c}} \right) \ge 0\) bằng cách quy mẫu thức nhiều phân thức.
Cách giải:
Ta có:
\(\begin{array}{l}\left( {\frac{a}{b} + \frac{b}{c} + \frac{c}{a}} \right) - \left( {\frac{b}{a} + \frac{c}{b} + \frac{a}{c}} \right)\\ = \left( {\frac{a}{b} - \frac{b}{a}} \right) + \left( {\frac{b}{c} - \frac{c}{b}} \right) + \left( {\frac{c}{a} - \frac{a}{c}} \right)\\ = \frac{{{a^2} - {b^2}}}{{ab}} + \frac{{{b^2} - {c^2}}}{{bc}} + \frac{{{c^2} - {a^2}}}{{ac}}\\ = \frac{{\left( {{a^2} - {b^2}} \right)c + \left( {{b^2} - {c^2}} \right)a + b\left( {{c^2} - {a^2}} \right)}}{{abc}}\\ = \frac{{{a^2}c - {b^2}c + {b^2}a - {c^2}a + b{c^2} - b{a^2}}}{{abc}}\\ = \frac{{\left( {{a^2}c - {c^2}a} \right) + \left( { - {b^2}c + {b^2}a} \right) + \left( {b{c^2} - b{a^2}} \right)}}{{abc}}\\ = \frac{{ac\left( {a - c} \right) + {b^2}\left( {a - c} \right) + b\left( {c - a} \right)\left( {c + a} \right)}}{{abc}}\\ = \frac{{ac\left( {a - c} \right) + {b^2}\left( {a - c} \right) - b\left( {a - c} \right)\left( {a + c} \right)}}{{abc}}\\ = \frac{{\left( {a - c} \right)\left[ {ac + {b^2} - b\left( {a + c} \right)} \right]}}{{abc}}\\ = \frac{{\left( {a - c} \right)\left( {ac + {b^2} - ba - bc} \right)}}{{abc}}\\ = \frac{{\left( {a - c} \right)\left[ {\left( {ac - bc} \right) + \left( {{b^2} - ba} \right)} \right]}}{{abc}}\\ = \frac{{\left( {a - c} \right)\left[ {c\left( {a - b} \right) - b\left( {a - b} \right)} \right]}}{{abc}}\\ = \frac{{\left( {a - c} \right)\left( {c - b} \right)\left( {a - b} \right)}}{{abc}}\end{array}\)
\( \Rightarrow \left( {\frac{a}{b} + \frac{b}{c} + \frac{c}{a}} \right) - \left( {\frac{b}{a} + \frac{c}{b} + \frac{a}{c}} \right) = \frac{{\left( {a - c} \right)\left( {c - b} \right)\left( {a - b} \right)}}{{abc}}\)
Vì \(0 < a \le b \le c\) suy ra
\(\left. \begin{array}{l}\left( {a - c} \right) \le 0\\\left( {a - b} \right) \le 0\\\left( {c - b} \right) \ge 0\end{array} \right\}\) \( \Rightarrow \left( {a - c} \right)\left( {a - b} \right)\left( {c - b} \right) \ge 0\)
Lại có: \(abc > 0\)
\( \Rightarrow \frac{{\left( {a - c} \right)\left( {c - b} \right)\left( {a - b} \right)}}{{abc}} \ge 0\)
Mà \(\left( {\frac{a}{b} + \frac{b}{c} + \frac{c}{a}} \right) - \left( {\frac{b}{a} + \frac{c}{b} + \frac{a}{c}} \right) = \frac{{\left( {a - c} \right)\left( {c - b} \right)\left( {a - b} \right)}}{{abc}}\) (chứng minh trên)
\( \Rightarrow \left( {\frac{a}{b} + \frac{b}{c} + \frac{c}{a}} \right) - \left( {\frac{b}{a} + \frac{c}{b} + \frac{a}{c}} \right) \ge 0\)
\( \Rightarrow \frac{a}{b} + \frac{b}{c} + \frac{c}{a} \ge \frac{b}{a} + \frac{c}{b} + \frac{a}{c}\) (đpcm)














Danh sách bình luận