Đề kiểm tra 45 phút (1 tiết ) - Đề số 1 - Chương 2 - Hình học 8

Đề bài

Bài 1.Tính diện tích của tam giác vuông cân biết cạnh huyền là 4 cm.

Bài 2. Cho hình thang ABCD \(\left( {AB// CD} \right)\) và AB < CD. Qua trung điểm M của cạnh bên BC kẻ đường thẳng song song với AD cắt CD ở E và AB ở F.

a) Chứng minh tứ giác AFED là hình bình hành.

b) Chứng minh \({S_{ADE}} = {S_{ABEC}} = \dfrac{1}{2}{S_{ABCD}}.\)

Bài 3. Cho tứ giác ABCD. Trên các tia đối của tia BA, CB, DC, AD lần lượt lấy các điểm E, F, G, H sao cho BE = BA, CF = CB, DG = DC và AH = AD. Chứng minh rằng: \({S_{ABCD}} = \dfrac{1}{ 5}{S_{EFGH}}.\)

LG bài 1

Phương pháp giải:

Đặt hai cạnh góc vuông AB, AC là x

Áp dụng định lý Py-ta-go

\({S_{ABC}} = {1 \over 2}AB.AC\)

Lời giải chi tiết:

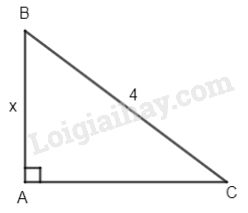
Đặt hai cạnh góc vuông AB, AC là x ta có: 

\({x^2} + {x^2} = {4^2}\) (định lý Py – ta – go)

\( \Rightarrow 2{x^2} = 16 \Rightarrow {x^2} = 8 \Rightarrow x = \sqrt 8 \left( {cm} \right)\)

Do đó: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}{\left( {\sqrt 8 } \right)^2} = 4\left( {c{m^2}} \right)\)

LG bài 2

Phương pháp giải:

Áp dụng: Tứ giác có 2 cặp cạnh đối song song là hình bình hành

Lời giải chi tiết:

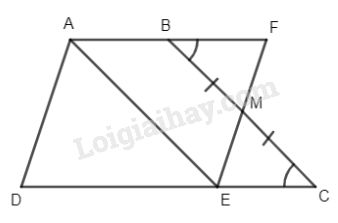
Ta có \(\Delta BFM = \Delta CEM\left( {c.g.c} \right) \)

\(\Rightarrow {S_{BFM}} = {S_{CEM}}\)

Do đó: \({S_{ABCD}} = {S_{AFED}}\)

AFED là hình bình hành (\(AF//DE\) và \(AD// FE\) )

\( \Rightarrow \Delta ADE = \Delta {\rm{EFA}}\left( {c.c.c} \right)\)

\( \Rightarrow {S_{ADE}} = {S_{EFA}} = {1 \over 2}{S_{AFED}} \)\(\,= {S_{ABME}} + {S_{BFM}} = {S_{ABME}} + {S_{CEM}}\)

Do đó: \({S_{ADE}} = {S_{ABEC}} = {1 \over 2}{S_{AFED}} = {1 \over 2}{S_{ABCD}}\)

LG bài 3

Phương pháp giải:

Hai tam giác có cùng chiều cao và độ dài cạnh đáy bằng nhau thì có diện tích bằng nhau

Lời giải chi tiết:

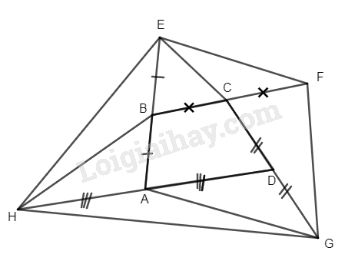
Ta có BA là trung tuyến của \(\Delta HBD\) nên \({S_{BAH}} = {S_{BAD}}.\)

HB là trung tuyến của \(\Delta HEA\) nên \({S_{BAH}} = {S_{BEH}}.\)

Do đó \({S_{HEA}} = 2{S_{BAD}}.\)

Chứng minh tương tự có:

\({S_{EFB}} = 2{S_{ABC}}\)

\({S_{CFG}} = 2{S_{BCD}}\)

\({S_{HDG}} = 2{S_{ADC}}\)

Mà \({S_{EFGH}} = {S_{HEA}} + {S_{EFB}} + {S_{CFG}} + {S_{HDG}} + {S_{ABCD}}\)

               \( = 2\left( {{S_{BAD}} + {S_{BCD}}} \right) + 2\left( {{S_{ABC}} + {S_{ADC}}} \right) + {S_{ABCD}}\)

               \( = 2{S_{ABCD}} + 2{S_{ABCD}} + {S_{ABCD}} = 5{S_{ABCD}}\)

\( \Rightarrow {S_{ABCD}} = \dfrac{1 }{ 5}{S_{EFGH}}.\)

Loigiaihay.com