Đề cương ôn tập học kì 1 toán 8

LT đại số

I. PHÉP NHÂN – PHÉP CHIA ĐA THỨC

1. Phép nhân:

a)Nhân đơn thức với đa thức:

A.(B + C) = A.B + A.C

b)Nhân đa thức với đa thức:

(A + B)(C + D) = A.B + A.C +B.C + B.D

2. Các hằng đẳng thức đáng nhớ:

1) (A + B)² = A² + 2AB + B²

2) (A - B)² = A² - 2AB + B²

3) A² – B² = (A – B)(A + B)

4) (A + B)³ = A³ + 3A²B + 3AB² + B³

5) (A - B)³ = A³ - 3A²B + 3AB² - B³

6) A³ + B³ = (A + B)(A² – AB + B²)

7) A³ - B³ = (A - B)(A² + AB + B²)

* Mở rộng:

(A + B – C)² = A² + B² + C² + 2AB – 2AC – 2BC

3. Phân tích đa thức thành nhân tử:

a) Phân tích đa thức thành nhân tử là biến đổi đa thức đó thành tích của những đơn thức và đa thức.

b) Các phương pháp cơ bản :

- Phương pháp đặt nhân tử chung.

- Phương pháp dùng hằng đẳng thức.

- Phương pháp nhóm các hạng tử.

* Chú ý: Khi phân tích đa thức thành nhân tử ta thường phối hợp cả 3 phương pháp

4. Phép chia:

a) Chia đơn thức cho đơn thức:

- Đơn thức A chia hết cho đơn thức B khi mỗi bíến của B đều là biến của A với số mũ bé hơn hoặc bằng số mũ của nó trong A.

- Qui tắc: Muốn chia đơn thức A cho đơn thức B(trường hợp chia hết) :

+ Chia hệ số của A cho hệ số B.

+ Chia từng lũy thừa của biến trong A cho lũy thừa của biến đó trong B.

+ Nhân các kết quả với nhau.

b) Chia đa thức cho đơn thức:

- Điều kiện chia hết: Đa thức A chia hết cho đơn thức B khi mỗi hạng tử của A đều chia hết cho B.

- Qui tắc: Muốn chia đa thức A cho đơn thức B (trường hợp chia hết) ta chia mỗi hạng tử của A cho B , rồi cộng các kết quả với nhau :

(M + N) : B = M : B + N : B

c) Chia hai đa thức một biến đã sắp xếp :

- Với hai đa thức A và B (B ≠ 0), luôn tồn tại hai đa thức duy nhất Q và R sao cho :

A = B.Q + R ( trong đó R = 0), hoặc bậc của R bé hơn bậc của B khi R ≠ 0.

- Nếu R = 0 thì A chia chia hết cho B.

II. PHÂN THỨC ĐẠI SỐ

1. Định nghĩa: Phân thức đại số là biểu thức có dang \(\frac{{\rm{A}}}{{\rm{B}}}\)(A, B là những đa thức, B ≠ 0).

2. Phân thức bằng nhau:

\(\frac{A}{B} = \frac{C}{D}{\rm{ }}\)nếu A.D = B.C

3. Tính chất cơ bản:

- Nếu đa thức M ≠ 0 thì \(\frac{A}{B} = \frac{{A.M}}{{B.M}}\)

- Nếu đa thức N là nhân tử chung thì \(\frac{A}{B} = \frac{{A:N}}{{B:N}}\)

- Quy tắc đổi dấu : \(\frac{A}{B} = \frac{{ - A}}{{ - B}}\)

4. Rút gọn phân thức : Gồm các bước

+ Phân tích tử và mẫu thành nhân tử (nếu có thể) để tìm nhân tử chung.

+ Chia cả tử và mẫu cho nhân tử chung.

5. Quy đồng mẫu thức nhiều phân thức:

+ Phân tích các mẫu thành nhân tử rồi tìm MTC.

+ Tìm nhân tử phụ của mỗi mẫu thức.

+ Nhân tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

6. Cộng các phân thức đại số :

a) Cộng các PTĐS cùng mẫu: Ta cộng tử thức với nhau, giữ nguyên mẫu thức rồi rút gọn PTĐS vừa tìm được.

b) Cộng các PTĐS không cùng mẫu: Ta qui đồng mẫu thức, rồi cộng các PTĐS cùng mẫu tìm được.

c) Phép cộng các PTĐS có các tính chất :

+ Giao hoán : \(\frac{A}{B} + \frac{C}{D} = \frac{C}{D} + \frac{A}{B}\)

+ Kết hợp : \((\frac{A}{B} + \frac{C}{D}) + \frac{E}{F} = \frac{A}{B} + (\frac{C}{D} + \frac{E}{F})\)

7. Trừ các phân thức đại số :

a) Hai phân thức gọi là đối nhau nếu tổng của chúng bằng 0 (\(\frac{A}{B}{\rm{ \,\text{và}\, - }}\frac{A}{B}\) là hai phân thức đối nhau)

b) Qui tắc đổi dấu : \( - \frac{A}{B} = \frac{{ - A}}{B} = \frac{A}{{ - B}}\)

c) Phép trừ : \(\frac{A}{B} - \frac{C}{D} = \frac{A}{B} + ( - \frac{C}{D})\)

8. Nhân các phân thức đại số :

a) Nhân các PTĐS ta nhân các tử thức với nhau, nhân các mẫu thức với nhau , rồi rút gọn PTĐS tìm được :

\(\frac{A}{B}.\frac{C}{D} = \frac{{A.C}}{{B.D}}\)

b) Phép nhân các PTĐS có tính chất :

+ Giao hoán : \(\frac{A}{B}.\frac{C}{D} = \frac{C}{D}.\frac{A}{B}\)

+ Kết hợp : \((\frac{A}{B}.\frac{C}{D}).\frac{E}{F} = \frac{A}{B}.(\frac{C}{D}.\frac{E}{F})\)

+ Phân phối đối với phép cộng :

\(\frac{A}{B}.(\frac{C}{D} + \frac{E}{F}) = \frac{A}{B}.\frac{C}{D} + \frac{A}{B}.\frac{E}{F}\)

9. Chia các phân thức đại số :

a) Hai phân thức được gọi là nghịch đảo lẫn nhau nếu tích của chúng bằng 1.

\(\frac{A}{B}{\rm{ \,\text{và}\, }}\frac{B}{A}\) là hai phân thức nghịch đảo lẫn nhau (với \(\frac{A}{B} \ne 0\))

b) Chia hai phân thức :

\(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C} = \frac{{A.D}}{{B.C}}{\rm{ }}\) (Với \(\frac{C}{D} \ne 0\))

10. Biểu thức hữu tỉ :

- Biểu thức chỉ chứa phép toán cộng, trừ , nhân , chia và chứa biến ở mẫu gọi là biểu thức hữu tỉ

- Điều kiện xác định của biểu thức hữu tỉ chỉ được xác định với điều kiện giá trị của mẫu thức khác 0

- Giá trị một biểu thức phân chỉ được xác định khi giá trị của mẫu thức khác 0.

LT hình học

I. TỨ GIÁC

1. Tứ giác: Tổng các góc trong của một giác bằng 360⁰.

2. Hình thang:

a) Hình thang là tứ giác có hai cạnh đối

song song

b) Hình thang có một góc vuông là hình thang vuông.

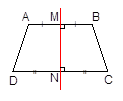
c) Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

*Trong hình thang cân :

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

*Dấu hiệu nhận biết :

- Hình thang có hai đường chéo bằng nhau.

- Hình thang có hai góc kề một đáy bằng nhau.

3. Đường trung bình của tam giác, của hình thang:

*Đường trung bình của tam giác thì song song với

cạnh thứ ba và bằng nữa cạnh ấy.

*Đường trung bình của hình thang thì song song với

hai đáy và bằng nửa tổng hai đáy.

4.Đối xứng trục:

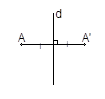
*Hai điểm A và A^’ là đối xứng nhau qua đường thẳng d nếu d là trung trực của AA^’.

*Đường thẳng, góc, tam giác đối xứng nhau qua một đường thẳng thì chúng bằng nhau.

*Hình thang cân nhận đường thẳng đi qua trung điểm của hai đáy làm trục đối xứng.

5. Hình bình hành:

*Hình bình hành là tứ giác có

các cạnh đối song song.

(hay hình bình hành là hình thang có hai cạnh bên song song)

*Trong hình bình hành :

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

*Dấu hiệu nhận biết :

+ Tứ giác có các cạnh đối song song.

+ Tứ giác có các cạnh đối bằng nhau.

+ Tứ giác có hai cạnh đối vừa song song vừa bằng nhau.

+ Tứ giác có các góc đối bằng nhau.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

6. Đối xứng tâm:

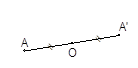
*Hai điểm A và A^’ gọi là đối xứng nhau qua điểm O

nếu O là trung điểm của AA^’

*Đường thẳng, góc, tam giác đối xứng nhau qua một điểm thì chúng bằng nhau.

*Hình bình hành nhận giao điểm của hai đường chéo làm tâm đối xứng.

7. Hình chữ nhật:

*Hình chữ nhật là tứ giác có 4 góc vuông.

*Trong hình chữ nhật : Hai đường chéo bằng nhau.

*Dấu hiệu nhận biết :

+ Tứ giác có 3 góc vuông.

+ Hình thang cân có một góc vuông.

+ Hình bình hành có một góc vuông.

+ Hình bình hành có hai đường chéo bằng nhau.

8. Trung tuyến của tam giác vuông

- Trong tam giác vuông , trung tuyến ứng với cạnh huyền bằng nữa cạnh huyền.

- Nếu một tam giác có trung tuyến ứng với một cạnh bằng nữa cạnh ấy thì tam giác đó là tam giác vuông.

9. Hình thoi:

*Hình thoi là tứ giác có 4 cạnh bằng nhau.

*Trong hình thoi :

+ Hai đường chéo vuông góc.

+ Hai đường chéo là phân giác của các góc của hình thoi.

*Dấu hiệu nhận biết :

+ Tứ giác có 4 cạnh bằng nhau.

+ Hình bình hành có 2 cạnh kề bằng nhau.

+ Hình bình hành có 2 đường chéo vuông góc.

+ Hình bình hành có 1 đường chéo là phân giác của một góc.

10. Hình vuông:

*Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.

*Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi

Dấu hiệu nhận biết :

+ Hình chữ nhật có 2 cạnh kề bằng nhau.

+ Hình chữ nhật có 2 đường chéo vuông góc.

+ Hình chữ nhật có 1 đường chéo là phân giác của một góc.

+ Hình thoi có 1 góc vuông.

+ Hình thoi có 2 đường chéo bằng nhau.

II. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC

- Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó

- Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau

- Diện tích hình chữ nhật bằng tích hai kích thước của nó: S= a.b

- Diện tích hình vuông bằng bình phương cạnh của nó: \(S = {a^2}\)

- Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông: \(S = \frac{1}{2}a.b\)

- Diện tích tam giác bằng nửa tích của 1 cạnh với chiều cao ứng với cạnh đó: \(S = \frac{1}{2}a.h\)

- Diện tích hình thang bằng nửa tích của nửa tổng hai đáy với chiều cao: \(S = \frac{1}{2}\left( {a + b} \right).h\)

- Diện tích hình bình hành bằng tích của một cạnh với chiều cao tương ứng với cạnh đó: \(S = a.h\)

- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{1}{2}{d_1}.{d_2}\)

BT đại số

Câu 1: Cho biết x²-3x(-2+2)=36 . Giá trị của x là :

A. 5 B. 6 C. -6 D. Cả B; C đều đúng

Câu 2: Giá trị của biểu thức A= 2x( 3x-1)-6x(x+1) –(3-8x) là :

A. –16x-3 B. –3 C. –16x D. Một đáp số khác

Câu 3 : Cho A= 3(2x-3)(3x+2)-2(x+4)(4x-3) + 9x(4-x) . Để A có giá trị bằng 0 thì giá trị của x là :

A. 2 B. 3 C. Cả A, B đều đúng D. Một đáp số khác

Câu 4: Giá trị của biểu thức A= x³ +3x²+3x+1 với x=99 là :

A. 1000000 B. 100000 C. 10000 D. Một kết quả khác

Câu5 : Giá trị của biểu thức A= x³–3x² +3x với x=11 là :

A. 999999 B. 99999 C. 9999 D. Một đáp số khác

Câu 6 : Biết 3x+2(5-x) = 0 . Giá trị của x là:

A. –8 B. –9 C. –10 D. Một đáp số khác

Câu 7: Cho biểu thức A=(3x-5)(2x+11) –(2x+3)(3x+7) Câu nào sau đây đúng

A. A = 6x²-15x-55 B. A = –43x –55

C. A không phụ thuộc vào x D. A = 2x-7

Câu 8: Để biểu thức 9x² +30x+a là bình phương của một tổng thì giá trị của a là :

A. 9 B. 25 C. 36 D. Một đáp số khác

Câu 9: Để biểu thức x² +ax +9 biểu diễn được dưới dạng bình phương của một tổng , giá trị của a là :

A. 3 B. 6 C. –6 D. Cả B, C

Câu 10 : Giá trị nhỏ nhất của biểu thức 4x² +12x +10 đạt được khi x bằng :

A. –1/2 B. –1 C. –3/2 D. Một đáp số khác

Câu 11: Với mọi giá trị của biến số giá trị của biểu thức 16x⁴ –40x²y³+ 25y⁶ là một số :

A. dương B. không dương

C. âm D. không âm

Câu 12: Câu nào sau đây sai:

a) x³-4x²+4x-1= (x-1)(x²-3x + 1)

b) x³-3x² +4x-2=(x-1)x²-2x+2)

c) x³-4x²+5x -2= (x-1)(x²-2x+2)

d) x³-3x² +2=(x-1)² (x-2)

Câu13:Nếu đa thức chia hết cho đa thức thì giá trị của a là:

A. -1 B. -2 C. -4 D. Một giá trị khác

Câu 14: Nếu đa thức cho x+5 có số dư bằng 2 thì a bằng:

A.10 B.15 C.20 D. Một giá trị khác

Câu 15 : Giá trị nhỏ nhất của biểu thức x²-4x+1 là :

A. -3 B. C. D. Một đáp số khác

Tự luận

Dạng 1: Thực hiện phép tính:

1) x²(x – 2x³)

2) 2xy(x²+ xy - 3y²)

3) (2x -3)² – 4x(x-3)

4) (3x² – 6x):3x

5) (x – 2)(x – x² + 4)

6) (2x² - \(\frac{1}{3}\)xy+ y²).(-3x³)

7) x(2x² – 3) – x²(5x + 1) + x².

8) (x + 2)(3x² - 4x)

9) (x³ + 3x² - 8x - 20) : (x + 2)

10) (4x² – 4x – 4) : (x + 4)

11) (2x³ – 3x² + x – 2) : (x + 5)

12) (x + y)² + (x – y)² – 2(x + y)(x - y)

13) (x – y)(x + y)(x² + y²)(x⁴ + y⁴)

14) 2x²(x – 2)+ 3x(x²– x – 2) –5(3 – x²)

15) (x – 1)(x – 3) – (4 – x)(2x + 1) – 3x² + 2x – 5

16) (x⁴ – x³ – 3x² + x + 2) : (x² – 1)

17) (x⁵ + 4x³ – 6x²) : 4x²

18) (x³ – 3x² + x – 3) : (x – 3)

19) (x³ – 8) : (x² + 2x + 4)

20) (2x⁴ – 5x² + x³ – 3 – 3x) : (x² – 3)

Dạng 2: Phân tích đa thức thành nhân tử

1) 1 – 2y + y²

2) (x + 1)² – 25

3) 1 – 4x²

4) 8 – 27x³

5) 27 + 27x + 9x² + x³

6) 8x³ – 12x²y + 6xy² – y³

7) 25 – x² + 4xy – 4y²

8) x³ + 8y³

9) 3x² – 6x + 9x²

10) 10x(x – y) – 6y(y – x)

11) 3x² + 5y – 3xy – 5x

12) 3y² – 3z² + 3x² + 6xy
13) 16x³ + 54y³

14) x² – 25 – 2xy + y²

15) 5x² – 10xy + 5y² – 20z²

16) 16x – 5x² – 3

17) x² – 5x + 5y – y²

18) 3x² – 6xy + 3y² – 12z²

19) x² + 4x + 3

20) x² – 5x + 4

21) 2x² + 3x – 5

22) (x² + 1)² – 4x²

23) x² – 4x – 5

24) x⁵ – 3x⁴ + 3x³ – x²

25) xy + y² – x – y

26) xy + xz – 2y – 2z

27) x² – 6xy + 9y² – 25z²

28) 3x² – 3y² - 12x + 12y

29) 4x³ + 4xy² + 8x²y – 16x

30) x⁴ – 5x² + 4

31) x³ – 2x² + 6x – 5

Dạng 3: Rút gọn biểu thức:

Bài 1: Cho phân thức: P = \(\frac{{3{x^2} + 3x}}{{(x + 1)(2x - 6)}}\)

a. Tìm điều kiện của x để P xác định.

b. Tìm giá trị của x để phân thức bằng 1.

Bài 2: Cho biểu thức \(C = \frac{x}{{2x - 2}} + \frac{{{x^2} + 1}}{{2 - 2{x^2}}}\)

a. Tìm x để biểu thức C có nghĩa.

b. Rút gọn biểu thức C.

c. Tìm giá trị của x để biểu thức có giá trị –0,5.

Bài 3: Cho biểu thức A = \(\frac{{{x^3} + 2{x^2} + x}}{{{x^3} - x}}\)

a. Tìm x để A được xác định.

b. Rút gọn A.

c. Tìm x để A = 2.

D. Tìm giá trị nguyên của x để giá trị tương ứng của A là một số nguyên.

Bài 4: Cho biểu thức B = \(\left( {\frac{{{x^2} + 1}}{{x + 1}} - 1} \right).\left( {\frac{4}{{x - 1}} - \frac{2}{x}} \right)\)

a. Tìm x để B có nghĩa.

b. Rút gọn B.

Bài 5: Cho biểu thức C = \(\frac{x}{{2x - 2}} + \frac{{{x^2} + 1}}{{2 - 2{x^2}}}\)

a. Tìm x để C có nghĩa.

b. Rút gọn C

c. Tìm x để C = \( - \frac{1}{2}\)

d. Tìm số thực x để giá trị tương ứng của C là một số nguyên.

Bài 6: Cho biểu thức D = \(\frac{{3(x + 1)}}{{{x^3} + {x^2} + x + 1}}\)

a. Tìm x để D được xác định.

c. Rút gọn D.

c. Tìm x để D nhận giá trị nguyên.

d. Tìm giá trị lớn nhất của D.

Bài 7: Cho hai biểu thức \(A = \frac{{{x^2} - 9}}{{3\left( {x + 5} \right)}}\) và \(B = \frac{x}{{x + 3}} + \frac{{2x}}{{x - 3}} - \frac{{3{x^2} + 9}}{{{x^2} - 9}}\) với \(x \ne - 5\,;\,x \ne \pm 3\)

a. Tính giá trị của biểu thức A khi x=2

b. Rút gọn biểu thức B

c. Cho P=A.B. Tìm giá trị nguyên của x để P có giá trị nguyên

Bài 8: Cho biểu thức \(A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}\,\,\,\,\left( {x \ne \pm 2} \right).\)

a. Rút gọn biểu thức A

b. Tính giá trị biểu thức A khi x=4

c. Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên dương

Dạng 4: Một số bài tập nâng cao

Bài 1: Cho \(a + b + c = 0\,\left( {a \ne 0\,;\,b \ne 0\,;\,c \ne 0} \right).\) Tính giá trị biểu thức:

\(A = \frac{{{a^2}}}{{{a^2} - {b^2} - {c^2}}} + \frac{{{b^2}}}{{{b^2} - {c^2} - {a^2}}} + \frac{{{c^2}}}{{{c^2} - {a^2} - {b^2}}}\)

Bài 2: Cho \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\) và a,b,c là ba số khác 0.

Chứng minh: \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{3}{{abc}}\)

Bài 3: Cho số x,y thả mãn đẳng thức \(5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0\) Tính giá trị biểu thức:

\(M = {\left( {x + y} \right)^{2007}} + {\left( {x - 2} \right)^{2008}} + {\left( {y - 1} \right)^{2009}}\)

Bài 4: Cho xyz=2006

Chứng minh rằng: \(\frac{{2006x}}{{xy + 2006x + 2006}} + \frac{y}{{yz + y + 2006}} + \frac{z}{{xz + z + 1}} = 1\)

Bài 5: Cho x và y thỏa mãn \({x^2} + 2xy + 6x + 6y + 2{y^2} + 8 = 0\) Tìm GTLN và GTNN của biểu thức \(B = x + y + 2016\)

BT hình học

Câu 1: Cho tứ giác ABCD có \(\widehat A = {110^0},\,\widehat B = {70^0}\) .Gọi E là giao điểm của các phân giác trong của góc A và góc B. Số đo của góc AEB là:

A. 60⁰ B. 80⁰ C. 90⁰ D. 100⁰

Câu 2: Cho tứ giác ABCD, có . Số đo của góc C và góc D lần lượt là:

A. 60⁰và 50⁰ B. 70⁰và 60⁰

C. 80⁰và 70⁰ D. 90⁰và 80⁰

Câu 3: Cho hình thang cân có một trong các góc bằng 60⁰và các đáy có độ dài 15 cm và 49 cm. Chu vi hình thang cân là :

A. 128 cm B. 130 cm C. 132 cm D. 134 cm

Câu 4: Cho tam giác ABC từ M, N là trung điểm các cạnh AB, AC. Vẽ MI và NK cùng vuông góc với BC. Tìm câu sai :

A. MI//NK B. MI=NK C. MI=MN D. MN=IK

Câu 5: Cho ABC có chu vi là 27 cm. Gọi M,N,P là trung điểm các cạnh AB, BC , CA

Biết AB:BC:CA= 2:3:4 . Chiều dài các cạnh của NMP là :

A. 2,4 cm; 3,6 cm; 4,8 cm B. 3cm; 4,5 cm; 6cm

C. 4 cm; 6cm ; 8cm D. 5cm; 7,5cm; 10cm

Câu 6: Các điểm A,B,C thẳng hàng theo thứ tự đó và đối xứng các điểm A’,B’,C’ qua một đường thẳng d. Biết BC = 4 cm và AB = 13cm . Độ dài A’C’ là :

A. 15cm B. 16cm C. 17cm D. 18cm

Câu 7 : Trong các câu sau câu nào đúng . Có hình bình hành ABCD thỏa :

A. Tất cả các góc đều nhọn B. Â nhọn còn góc B tù

C. Góc B và góc C đều nhọn D. Â = 90⁰ còn góc B nhọn

Câu 8 : Trong các câu sau câu nào sai. Có hình bình hành có hai góc có số đo là :

A. 40⁰ và 50⁰ B. 30⁰ và 150⁰

C. 60⁰ và 120⁰ D. 55⁰ và 125⁰

Câu 9: Cho tam giác ABC đều . Từ điểm M thuộc miền trong của rABC kẻ đường thẳng song song với BC cắt AB ở D; đường thẳng song song với AC cắt BC ở E ; đường thẳng song song với AB căt AC ở F. Câu nào sau đây sai:

A. Các tứ giác BDME; CFME; ADMF là các hình thang cân

B. Chi vi tam giác DEF bằng tổng các khoảng cách từ điểm M đến các đỉnh của tam giác ABC

C. Tam giác DEF đều

D. \(\widehat {DME} = \widehat {DMF} = \widehat {EMF}\)

Câu 10: Cho tứ giác ABCD, Gọi E, F , G, H theo thứ tự là trung điểm cuỉa các cạnh AD,AB, BC, CD và I, J là trung điểm của các đường chéo AC và BD. Câu nào sau đây sai:

A. EHGF là hình thoi B. HIFJ là hình thoi

C. EIGJ là hình thoi D. EG; HF ; IJ đồng qui

Câu11: Cho tam giác ABC, Trong đó AB = 11,5cm, AC = 6cm. Vẽ hình đối xứng với tam giác đã cho qua trung điểm của cạnh BC. Chu vi của tứ giác tạo thành là :

A. 12,1cm B. 33cm C. 34cm D. 35cm

Câu 13: Đường chéo của hình vuông thứ nhất dài 4m, cạnh của hình vuông này là đường chéo của hình vuông thứ hai. Độ dài của cạnh hình vuông thứ hai là:

A. 4m B. \(2\sqrt 2 \)m C. 2m D. Một kết quả khác

Tự luận

Bài 1: Tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm AC, K là điểm đối xứng của M qua I.

Tứ giác AMCK là hình gì? Vì sao?
Tứ giác AKMB là hình gì? Vì sao?
Trên tia đối của tia MA lấy điểm L sao cho ML = MA. Chứng minh tứ giác ABEC là hình thoi

Bài 2: Cho Tam giác ABC vuông ở C. Gọi M, N lần lượt là trung điểm của các cạnh BC và AB. Gọi P là điểm đối xứng của M qua N.

Chứng minh tứ giác MBPA là hình bình hành
Chứng minh tứ giác PACM là hình chữ nhật
Đường thẳng CN cắt PB ở Q. Chứng minh BQ = 2PQ
Tam giác ABC cần có thêm điều kiện gì thì hình chữ nhật PACM là hình vuông?

Bài 3: Cho hình bình hành ABCD có , AD = 2AB. Gọi M là trung điểm của AD, N là trung điểm của BC.

Chứng minh tứ giác MNCD là hình thoi
Từ C kẻ đường thẳng vuông góc với MN tại E, cắt AB tại F. Chứng minh E là trung điểm của CF
Chứng minh DMCF đều
Chứng minh ba điểm F, N, D thẳng hàng.

Bài 4: Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC

Chứng minh BC = 2MN
Gọi K là điểm đối xứng của M qua N. Tứ giác BCKM là hình gì? Vì sao?
Tứ giác AKCM là hình gì? Vì sao?
Để tứ giác AKCM là hình chữ nhật thì tam giác ABC cần có thêm điều kiện gì?

Bài 5: Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Qua B vẽ đường thẳng song song với AC. Qua C vẽ đường thẳng song song với BD, chúng cắt nhau tại I.

Chứng minh OBIC là hình chữ nhật
Chứng minh AB = OI
Tìm điều kiện của hình thoi ABCD để tứ giác OBIC là hình vuông.

Bài 6: Cho tam giác ABC vuông tại A (AB < AC., trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA

Tứ giác ABDC là hình gì? Vì sao?
Gọi I là điểm đối xứng của A qua BC. Chứng minh BC // ID
Chứng minh tứ giác BIDC là hình thang cân
Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh AM vuông góc với EF

Bài 7: Cho tam giác ABC vuông tại A và D là trung điểm BC. Gọi M là điểm đối xứng của D qua AB. E là giao điểm của DM và AB. Gọi N là điểm đối xứng của D qua AC, F là giao điểm của DN và AC.

Tứ giác AEDF là hình gì? Vì sao?
Tứ giác ADBM là hình gì? Vì sao?
Chứng minh M đối xứng với N qua A
Tam giác vuông ABC cần có thêm điều kiện gì thì tứ giác AEDF là hình vuông?

Bài 8: Cho tam giác ABC vuông tại A, có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.

Chứng minh tứ giác AEBM là hình thoi.
Gọi I là trung điểm của AM. Chứng minh E, I, C thẳng hàng.
Tam giác ABC có thêm điều kiện gì thì AEBM là hình vuông.

Bài 9: Cho \(\Delta ABC\) các đường trung tuyến BD và CE cắt nhau tại G. Gọi H là trung điểm của GB, K là trung điểm của GC.

Chứng minh tứ giác DEHK là hình bình hành.
\(\Delta ABC\) có điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
Nếu BD vuông góc với CE thì tứ giác DEHK là hình gì ?

Bài 10: Cho hình bình hành ABCD có AD = 2.AB , \(\widehat A = {60^ \circ }\). Gọi E, F lần lượt là trung điểm của BC và AD .

Chứng minh : AE \( \bot \) BF.
Chứng minh : BFDC là hình thang cân.
Tính \(\widehat {ADB}\).
Lấy M đối xứng với A qua B. Chứng minh tứ giác BMCD là hình chữ nhật. Suy ra M, E, D thẳng hàng.