-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
Bài tập 12 trang 90 Tài liệu dạy – học Toán 8 tập 2
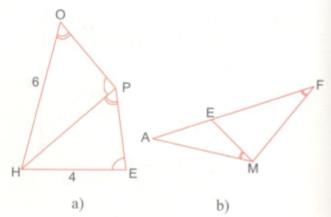
Giải bài tập a) Hình a, cho biết
Đề bài
a) Hình a, cho biết \(\widehat O = \widehat {HPE};\,\,\widehat {HPO} = \widehat E;\,\,\,OH = 6;\)\(\,\,HE = 4.\) Tính HP.
b) Hình b, cho biết \(\widehat {AME} = \widehat {AFM.}\) Chứng minh: AM2 = AE.AF.
Lời giải chi tiết
a) Xét hai tam giác OHP và HPE có: \(\widehat O = \widehat {HPE}(gt)\) và \(\widehat {HPO} = \widehat E(gt)\)
Do đó \(\Delta OHP \sim \Delta PHE(g.g)\)
\(\Rightarrow {{OH} \over {PH}} = {{HP} \over {HE}}\)
\(\Rightarrow {6 \over {HP}} = {{HP} \over 4}\)
\(\Rightarrow H{P^2} = 24 \Rightarrow HP = 2\sqrt 6 \)
b) Xét ∆AME và ∆AFM ta có: \(\widehat {AME} = \widehat {AFM}(gt)\) và \(\widehat {EAM}\) chung
\( \Rightarrow \Delta AME \sim \Delta AFM(g.g)\)
\(\Rightarrow {{AM} \over {AF}} = {{AE} \over {AM}}\)
\(\Rightarrow A{M^2} = AE.AF\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 13 trang 90 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 14 trang 90 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 15 trang 90 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 16 trang 91 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 17 trang 91 Tài liệu dạy – học Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
