Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).

Trả lời câu hỏi 3 Bài 2 trang 35 Toán 9 Tập 2


Cho hàm số

Đề bài

Cho hàm số \(y = \displaystyle{{ - 1} \over 2}{x^2}\)

a) Trên đồ thị của hàm số này, xác định điểm D có hoành độ bằng \(3.\) Tìm tung độ của điểm D bằng hai cách: bằng đồ thị; bằng cách tính \(y\) với \(x = 3\). So sánh hai kết quả.

b) Trên đồ thị làm số này, xác định điểm có tung độ bằng \(-5.\) Có mấy điểm như thế ? Không làm tính, hãy ước lượng giá trị hoành độ của mỗi điểm.

Phương pháp giải - Xem chi tiết

a) Cách 1: Vẽ đồ thị hàm số \(y=-\dfrac{1}{2}x^2\). Trên đồ thị đã vẽ, từ điểm có hoành độ \(3\) trên trục \(Ox\) ta kẻ đường vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(D,\) từ  điểm \(D\) đó ta kẻ đường thẳng vuông góc với trục \(Oy\) cắt \(Oy\) tại đâu thì đó là tung độ của điểm \(D.\) 

Cách 2: Thay \(x=3\) vào hàm số \(y=-\dfrac{1}{2}x^2\) ta tìm được \(y\) từ đó suy ra tung độ điểm \(D\)

b) Trên đồ thị đã vẽ, từ điểm có tung độ là \(-5\) trên trục \(Oy\) ta kẻ đường vuông góc với \(Oy\) cắt đồ thị hàm số tại hai điểm,  từ  điểm mỗi điểm đó ta kẻ đường thẳng vuông góc với trục \(Ox\) cắt \(Ox\) tại đâu thì đó là hoành độ độ cần tìm.

Lời giải chi tiết

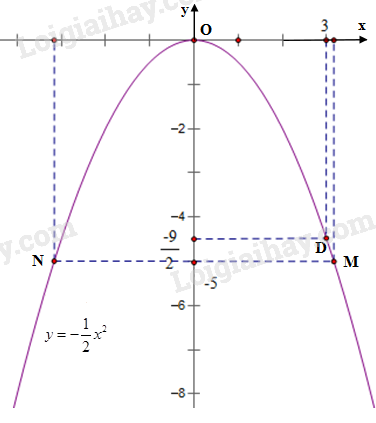
a) Từ đồ thị, ta xác định được tung độ của điểm D là \(\displaystyle{{ - 9} \over 2}\)

Với \(x = 3\) ta có: \(y = \displaystyle{{ - 1} \over 2}{x^2} = {\displaystyle{ - 1} \over 2}{.3^2} = {{ - 9} \over 2}\) 

Hai kết quả bằng nhau. 

b) Có 2 điểm có tung độ bằng \(-5\) là điểm \(M\) và điểm \(N\) (hình vẽ).

Giá trị của hoành độ điểm \(M\) là \( x_M\approx 3,2\) và hoành độ điểm \(N\) là \( x_N\approx -3,2\)


Bình chọn:
4 trên 25 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store