 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).
Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).
Bài 9 trang 39 SGK Toán 9 tập 2
Cho hai hàm số
Đề bài
Cho hai hàm số \(y = \dfrac{1 }{3}{x^2}\) và \(y = -x + 6\).
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số \(y=ax^2\):
Bước 1: Xác định 2 điểm thuộc đồ thị và các điểm đối xứng của chúng qua \(Oy\).
Bước 2: Vẽ parabol đi qua gốc \(O(0;0)\) và các điểm trên.
+) Cách vẽ đồ thị hàm số \(y=ax+b\):
Cho \(x=0 \Rightarrow y=b\). Đồ thị hàm số đi qua điểm \(A(0; b)\).
Cho \(y=0 \Rightarrow x =\dfrac{-b}{a}\). Đồ thị hàm số đi qua điểm \(B{\left(\dfrac{-b}{a}; 0 \right)}\)
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
b) Tìm tọa độ giao điểm của hai đồ thị hàm số \(y=ax+b\) và \(y=a'x^2\). Ta xét phương trình hoành độ giao điểm: \(ax+b=a'x^2\). Giải phương trình này tìm được hoành độ giao điểm. Thay giá trị đó vào công thức hàm số tìm được tung độ giao điểm.
Lời giải chi tiết
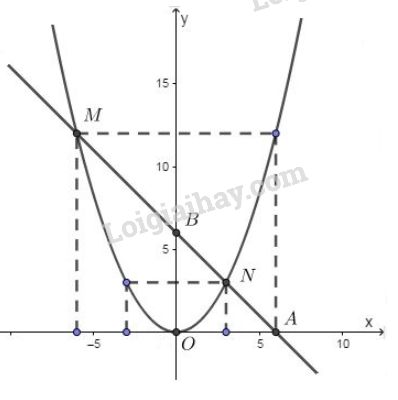
a) *Vẽ đồ thị: \(y = \dfrac{1 }{3}{x^2}\).
Bảng giá trị:
|
\(x\) |
\(-6\) |
\(-3\) |
\(0\) |
\(3\) |
\(6\) |
|
\(y=\dfrac{1}{3}x^2\) |
\(12\) |
\(3\) |
\(0\) |
\(3\) |
\(12\) |
Vẽ parabol đi qua gốc tọa độ và các điểm có tọa độ \(\left( { - 6;12} \right),\left( { - 3;3} \right),\left( {3;3} \right),\left( {6;12} \right)\) ta được đồ thị hàm số \(y = \dfrac{1 }{3}{x^2}\).
*Vẽ đồ thị: \(y = -x + 6\)
- Cho \(x = 0 \Rightarrow y = 0+6=6\). Đồ thị đi qua \(B(0; 6)\).
- Cho \(y = 0 \Rightarrow 0= -x+6 \Rightarrow x=6\). Đồ thị hàm số đi qua \(A(6; 0)\).
Đồ thị hàm số \(y=-x+6\) là đường thẳng đi qua hai điểm \(A,B\).
Vẽ đồ thị: xem hình bên dưới.
b) Xét phương trình hoành độ giao điểm:
\(\dfrac{1}{3}x^2=-x+6\)
\(\Leftrightarrow \dfrac{1}{3}x^2 +x -6=0\)
\(\Leftrightarrow x^2+3x-18=0\)
\(\begin{array}{l}\Leftrightarrow{x^2} - 3x + 6x - 18 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 6\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x + 6} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 6 = 0\\x - 3 = 0\end{array} \right.\end{array}\)
\( \Leftrightarrow \left[ \matrix{
x = -6 \hfill \cr
x = 3 \hfill \cr} \right.\)
Với \(x=3 \Rightarrow y=-3+6=3\). Đồ thị hàm số đi qua điểm \(N(3;3)\).
Với \(x=-6 \Rightarrow y=-(-6)+6=12\). Đồ thị hàm số đi qua điểm \(M(-6;12)\).
Vậy giao điểm của hai đồ thị là \(N(3;3)\) và \(M(-6;12)\).
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận