Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).

Bài 8 trang 38 SGK Toán 9 tập 2


Biết rằng đường cong trong hình 11 là

Đề bài

Biết rằng đường cong trong hình 11 là một parabol \(y = a{x^2}\).

a) Tìm hệ số \(a\).

b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = -3\).

c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).

 

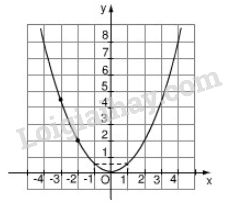
                    Hình 11

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Tìm tọa độ của một điểm bất kỳ thuộc hàm số \(y=ax^2\). Thay tọa độ điểm đó vào công thức hàm số, ta tìm được \(a\).

b) Thay \(x=x_0\) vào công thức hàm số \(y=ax^2\) ta tìm được \(y\).

c) Thay \(y=y_0\) vào công thức hàm số \(y=ax^2\). Giải phương trình này ta tìm được \(x\).

Lời giải chi tiết

a) Theo hình vẽ, ta lấy điểm \(A(-2; 2)\) thuộc đồ thị. Thay \(x = -2, y = 2\) vào công thức hàm số \(y=ax^2\), ta được:

 \(2 = a.{( - 2)^2} \Leftrightarrow a = \dfrac{1}{2}\).

Vậy hàm số có dạng: \(y=\dfrac{1}{2}x^2\).

b) Thay \(x=-3\) vào công thức hàm số \(y=\dfrac{1}{2}x^2\), ta được:

\(y=\dfrac{1}{2}.(-3)^2=\dfrac{1}{2}.9=\dfrac{9}{2}.\)

Vậy tung độ cần tìm là \(\dfrac{9}{2}\).

c) Thay \(y=8\) vào công thức đồ thị hàm số, ta được:

\(8 = \dfrac{1}{ 2}{x^2} \Leftrightarrow {x^2} = 16 \Leftrightarrow x =  \pm 4\)

Ta được hai điểm và tọa độ của hai điểm đó là \(M(4; 8)\) và \(M'(-4; 8)\).

loigiaihay.com


Bình chọn:
4.3 trên 94 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store