-
Bài 9.2 phần bài tập bổ sung trang 95 SBT toán 8 tập 1
Giải bài 9.2 phần bài tập bổ sung trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.
-
Bài 9.3 phần bài tập bổ sung trang 95 SBT toán 8 tập 1
Giải bài 9.3 phần bài tập bổ sung trang 95 sách bài tập toán 8. Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.
-
Bài 123 trang 95 SBT toán 8 tập 1
Giải bài 123 trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM...
-
Bài 122 trang 95 SBT toán 8 tập 1
Giải bài 122 trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.
-
Bài 121 trang 95 SBT toán 8 tập 1
Giải bài 121 trang 95 sách bài tập toán 8. Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DH
-
Bài 120 trang 95 SBT toán 8 tập 1
Giải bài 120 trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
-
Bài 119 trang 94 SBT toán 8 tập 1
Giải bài 119 trang 94 sách bài tập toán 8. Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.
-
Bài 118 trang 94 SBT toán 8 tập 1
Giải bài 118 trang 94 sách bài tập toán 8. Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
-
Bài 117 trang 94 SBT toán 8 tập 1
Giải bài 117 trang 94 sách bài tập toán 8. Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.
-
Bài 116 trang 94 SBT toán 8 tập 1
Giải bài 116 trang 94 sách bài tập toán 8. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính các độ dài AD, AB (làm tròn đến hàng đơn vị).
-
Bài 115 trang 94 SBT toán 8 tập 1
Giải bài 115 trang 94 sách bài tập toán 8. Tứ giác BEDC là hình gì ? Vì sao ?
-
Bài 114 trang 94 SBT toán 8 tập 1
Giải bài 114 trang 94 sách bài tập toán 8. Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC...
-
Bài 113 trang 94 SBT toán 8 tập 1
Giải bài 113 trang 94 sách bài toán toán 8. Các câu sau đúng hay sai ?
a) Hình chữ nhật là tứ giác có tất cả các góc bằng nhau...
-
Bài 112 trang 94 SBT toán 8 tập 1
Giải bài 112 trang 94 sách bài tập toán 8. Tìm các hình chữ nhật trên hình 17 (trong hình 17b, O là tâm của đường tròn)
-
Bài 111 trang 94 SBT toán 8 tập 1
Giải bài 111 trang 94 sách bài tập toán 8. Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm các cạnh AB, BC, CD, DA . Tứ giác EFGH là hình gì? Vì sao?
-
Bài 110 trang 93 SBT toán 8 tập 1
Giải bài 110 trang 93 sách bài tập toán 8. Chứng minh rằng các tia phân giác các góc của một hình bình hành cắt nhau tao thành một hình chữ nhật.
-
Bài 109 trang 93 SBT toán 8 tập 1
Giải bài 109 trang 93 sách bài tập toán 8. Tính x trên hình 16 (đơn vị đo : cm)
-
Bài 108 trang 93 SBT toán 8 tập 1
Giải bài 108 trang 93 sách bài tập toán 8. Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm (làm tròn kết quả đến chữ số thập phân thứ nhất)
-
Bài 107 trang 93 SBT toán 8 tập 1
Giải bài 107 trang 93 sách bài tập toán 8. Chứng minh rằng trong hình chữ nhật: a) Giao điểm của hai đường chéo là tâm đối xứng của hình...
-
Bài 106 trang 93 SBT toán 8 tập 1
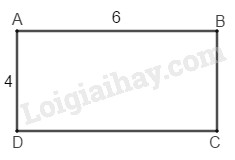
Giải bài 106 trang 93 sách bài tập toán 8. Tính đường chéo d của một hình chữ nhật, biết độ dài các cạnh a = 3cm, b = 5cm (làm tròn kết quả đến chữ số thập phân thứ nhất).













Danh sách bình luận