Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2 Bài 9. Hình chữ nhật

Bài 116 trang 94 SBT toán 8 tập 1


Giải bài 116 trang 94 sách bài tập toán 8. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính các độ dài AD, AB (làm tròn đến hàng đơn vị).

Đề bài

Cho hình chữ nhật \(ABCD.\) Gọi \(H\) là chân đường vuông góc kẻ từ \(A\) đến \(BD.\) Biết \(HD = 2cm,\, HB = 6cm.\) Tính các độ dài \(AD,\, AB\) (làm tròn đến hàng đơn vị).

Phương pháp giải - Xem chi tiết

Tính chất hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Định lý Py - ta - go trong tam giác ABC vuông tại A: \(AB^2+AC^2=BC^2\)

Lời giải chi tiết

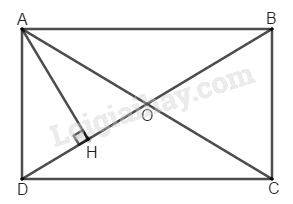
Ta có: \(DB = HD + HB = 2 + 6 = 8\,(cm)\)

Vì ABCD là hình chữ nhật nên theo tính chất hình chữ nhật, ta có: 

+ \(AC = DB\) 

+ \(OA = OB = OC = OD \)\(= \dfrac{1}{2} BD = 4\) \((cm)\)

Lại có \(OD = OH + HD\)

\(⇒ OH = OD – HD = 4 – 2 = 2\,(cm)\)

Suy ra \(HO = HD = 2\,(cm)\) nên H là trung điểm của OD

Kết hợp với \(AH ⊥ OD\)  

Khi đó, tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên \(∆ ADO\) cân tại \(A\)

\(⇒ AD = AO = 4\,(cm)\)

Trong tam giác vuông \(ABD\) có \(\widehat {BAD} = {90^0}\), ta có: 

\(B{D^2} = A{B^2} + A{D^2}\) (định lý Py-ta-go) \( \Rightarrow A{B^2} = B{D^2} - A{D^2}\)

\(AB = \sqrt {B{D^2} - A{D^2}} \) \(= \sqrt {{8^2} - {4^2}}  = \sqrt {48}  \approx 7\) \((cm)\)

Loigiaihay.com


Bình chọn:
4.2 trên 16 phiếu
Bài tiếp theo
  • Bài 117 trang 94 SBT toán 8 tập 1

    Giải bài 117 trang 94 sách bài tập toán 8. Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.

  • Bài 118 trang 94 SBT toán 8 tập 1

    Giải bài 118 trang 94 sách bài tập toán 8. Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.

  • Bài 119 trang 94 SBT toán 8 tập 1

    Giải bài 119 trang 94 sách bài tập toán 8. Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.

  • Bài 120 trang 95 SBT toán 8 tập 1

    Giải bài 120 trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.

  • Bài 121 trang 95 SBT toán 8 tập 1

    Giải bài 121 trang 95 sách bài tập toán 8. Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DH

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store