Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2 Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều

Bài 77 trang 155 SBT toán 8 tập 2


Giải bài 77 trang 155 sách bài tập toán 8. Thùng của một xe tải có dạng một hình lăng trụ đứng theo các kích thước cho ở hình 158.

Đề bài

Thùng của một xe tải có dạng một hình lăng trụ đứng theo các kích thước cho ở  hình 158:

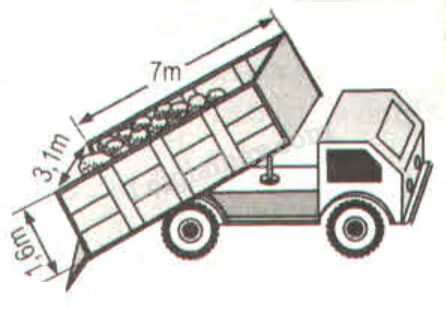
a) Tính thể tích của thùng chứa.

b) Nếu \(1m^3\) cát nặng \(1,6\) tấn và xe chở đến \(\displaystyle {3 \over 4}\) trọng tải của nó thì sức nặng cát lúc đó là bao nhiêu?

c) Khi cát được san phẳng chở đầy thì phần diện tích của nó bên trong thùng xe là bao nhiêu?

Phương pháp giải - Xem chi tiết

Sử dụng:

- Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.

\({S_{xq}} = 2p.h\)

Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao.

- Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.

\(V = S. h\)

Trong đó: \(S\) là diện tích đáy, \(h\) là chiều cao của lăng trụ.

Lời giải chi tiết

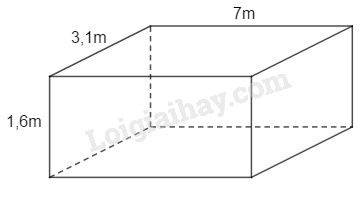
a) Thể tích của thùng chứa là: \(V = 3,1.7.1,6 = 34,72\;({m^3})\)

b) Phần thể tích chở cát là: \(\displaystyle 34,72.{3 \over 4} = 26,04\;({m^3})\)

Lượng cát nặng số tấn là: \(26,04.1,6 = 41,664\) (tấn)

c) Khi cát san phẳng chở đầy thì diện tích của nó bên trong thùng gồm diện tích xung quanh của hình hộp chữ nhật có kích thước là \(3,1m; 7m\) và \(1,6m\) cùng với đáy hình chữ nhật kích thước bằng \(3,1m\) và \(7m.\)

Diện tích xung quanh hình hộp chữ nhật là: \(S_{xq}=2.\left( {7 + 3,1} \right).1,6=32,32\,m^2\)

Diện tích đáy là: \(S_đ=3,1.7 =21,7\,m^2\)

Diện tích cát bên trong thùng là:

\(32,32 +21,7 = 54,02\)\(\;({m^2})\).

Loigiaihay.com


Bình chọn:
3.8 trên 4 phiếu
Bài tiếp theo
  • Bài 78 trang 155 SBT toán 8 tập 2

    Giải bài 78 trang 155 sách bài tập toán 8. Độ dài đường chéo AC1 (h.160) của một hình lập phương là căn 12 ...

  • Bài 79 trang 155 SBT toán 8 tập 2

    Giải bài 79 trang 155 sách bài tập toán 8. Nếu theo quy luật này thì có bao nhiêu hình lập phương đơn vị ở hình thứ 10?

  • Bài 80 trang 156 SBT toán 8 tập 2

    Giải bài 80 trang 156 sách bài tập toán 8. Hãy tìm diện tích mặt ngoài theo các kích thước cho ở hình 162. Biết rằng hình a gồm một hình chóp đều và một hình hộp chữ nhật, hình b gồm hai hình chóp đều.

  • Bài 81 trang 156 SBT toán 8 tập 2

    Giải bài 81 trang 156 sách bài tập toán 8. Số hình lập phương đơn vị ở hình dưới đây (h.163) là bao nhiêu (mỗi hình lập phương nhỏ là một hình lập phương đơn vị)?

  • Bài 82 trang 156 SBT toán 8 tập 2

    Giải bài 82 trang 156 sách bài tập toán 8. Cho biết hộp có dạng hình hộp chữ nhật, độ dài đường chéo là 50cm. Hãy tìm các kích thước của hai hình hộp như vậy.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store