-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2
Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
Bài 4.1 phần bài tập bổ sung trang 158 SBT toán 8 tập 2
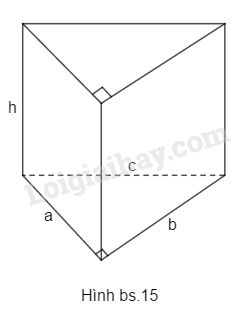
Bài 4.1 phần bài tập bổ sung trang 158 SBT toán 8 tập 2. Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:
Đề bài
Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:
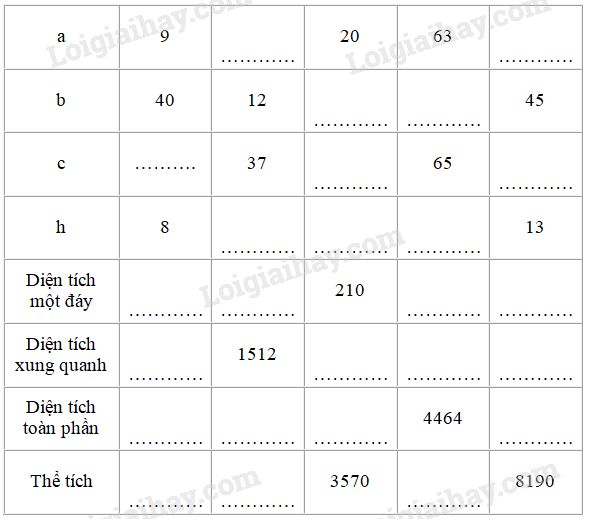
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
\({S_{xq}} = 2p.h\)
Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao.
- Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy.
- Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao
\(V = S. h\)
Trong đó: \(S\) là diện tích đáy; \(h\) là chiều cao lăng trụ.
- Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải chi tiết
Ta điền vào bảng như sau:
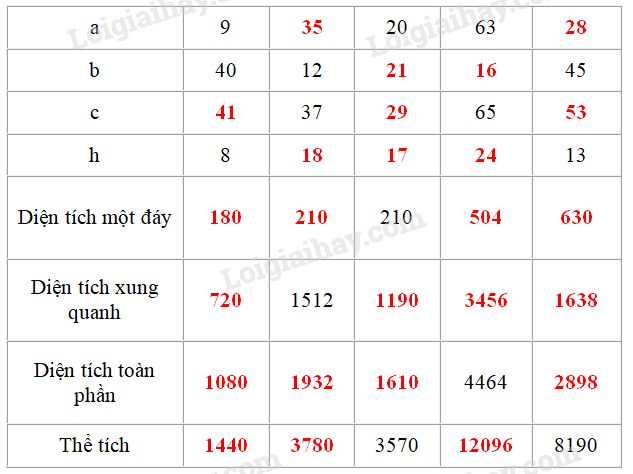
Giải thích:
Áp dụng định lí Pytago vào tam giác vuông đáy ta có: \({c^2} = {a^2} + {b^2}\)
- Với \(a=9;b=40;h=8\) ta có:
\(c = \sqrt {{9^2} + {{40}^2}} = 41\)
\({S_đ} = \dfrac{1}{2}.9.40 = 180\)
\({S_{xq}} = \left( {9 + 40 + 41} \right).8 = 720\)
\({S_{tp}} = 720 + 2.180 = 1080\)
\(V = 180.8 = 1440\)
- Với \(b=12;c=37;S_{xq}=1512\) ta có:
\(a = \sqrt {{{37}^2} - {{12}^2}} = 35\)
Ta có: \({S_{xq}} = \left( {35 + 12 + 37} \right).h = 1512\)
\(\Rightarrow h = 1512:84 = 18\)
\({S_đ} = \dfrac{1}{2}.35.12 = 210\)
\({S_{tp}} = 1512 + 2.210 = 1932\)
\(V = 210.18 = 3780\)
- Với \(a=20;S_đ=210;V=3570\) ta có:
\({S_đ} = \dfrac{1}{2}ab \Rightarrow b = \dfrac{{2{S_đ}}}{a} = \dfrac{{2.210}}{{20}} = 21\)
\(c = \sqrt {{{20}^2} + {{21}^2}} = 29\)
\(V = {S_đ}.h \Rightarrow h = \dfrac{V}{{{S_đ}}} = \dfrac{{3570}}{{210}} = 17\)
\({S_{xq}} = \left( {20 + 21 + 29} \right).17 = 1190\)
\({S_{tp}} = 1190 + 2.210 = 1610\)
- Với \(a=63;c=65;S_{tp}=4464\) ta có:
\(b = \sqrt {{{65}^2} - {{63}^2}} = 16\)
\({S_đ} = \dfrac{1}{2}ab = \dfrac{1}{2}.63.16 = 504\)
\({S_{tp}} = {S_{xq}} + 2{S_đ}\)
\(\Rightarrow {S_{xq}} = {S_{tp}} - 2{S_đ} \)\(\,= 4464 - 2.504 = 3456\)
Ta có: \({S_{xq}} = \left( {a + b + c} \right).h\)
\(\Rightarrow h = \dfrac{{{S_{xq}}}}{{a + b + c}} \)\(\,= \dfrac{{3456}}{{63 + 16 + 65}} = 24\)
\(V=504.24 = 12096\)
- Với \(b=45;h=13;V=8190\) ta có:
\(V = {S_đ}.h \) \(\Rightarrow {S_đ} = V:h = 8190:13 = 630\)
\({S_đ} = \dfrac{1}{2}ab \) \(\Rightarrow a = \dfrac{{2{S_đ}}}{b} = \dfrac{{2.630}}{{45}} = 28\)
\(c = \sqrt {{{28}^2} + {{45}^2}} = 53\)
\({S_{xq}} = \left( {28 + 45 + 53} \right).13 = 1638\)
\({S_{tp}} = 1638 + 2.630 = 2898\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4.2 phần bài tập bổ sung trang 158 SBT toán 8 tập 2
- Bài 4.3 phần bài tập bổ sung trang 158 SBT toán 8 tập 2
- Bài 4.4 phần bài tập bổ sung trang 159 SBT toán 8 tập 2
- Bài 4.5 phần bài tập bổ sung trang 159 SBT toán 8 tập 2
- Bài 90 trang 157 SBT toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
