Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2 Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều

Bài 4.3 phần bài tập bổ sung trang 158 SBT toán 8 tập 2


Giải bài 4.3 phần bài tập bổ sung trang 158 sách bài tập toán 8. Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng ...

Lựa chọn câu để xem lời giải nhanh hơn

Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng

LG a

Gấp đôi chiều cao của hình chóp;

Phương pháp giải:

Sử dụng:

- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.

\(V = \dfrac{1}{3} .S.h\)

Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

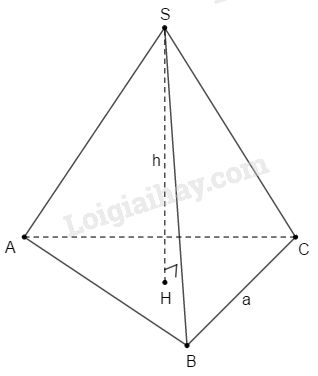
Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:

\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)

Nếu tăng gấp đôi chiều cao thì thể tích hình chóp là:

\(\displaystyle V' = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.2h = 2.{{{a^2}h\sqrt 3 } \over {12}} = 2V\)

LG b

Gấp đôi cạnh đáy của hình chóp;

Phương pháp giải:

Sử dụng:

- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.

\(V = \dfrac{1}{3} .S.h\)

Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:

\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)

Nếu tăng gấp đôi cạnh đáy thì thể tích hình chóp là:

\(\displaystyle V' = {1 \over 3}.{{{{\left( {2a} \right)}^2}\sqrt 3 } \over 4}.h = 4.{{{a^2}h\sqrt 3 } \over {12}} \)\(\,= 4V\)

LG c

Gấp đôi cả chiều cao và cạnh đáy của hình chóp.

Phương pháp giải:

Sử dụng:

- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.

\(V = \dfrac{1}{3} .S.h\)

Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).

Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:

\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)

Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là:

\(\displaystyle V' = {1 \over 3}.{{{{\left( {2a} \right)}^2}\sqrt 3 } \over 4}.2h = 8.{{{a^2}h\sqrt 3 } \over {12}} \)\(\,= 8V\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài 4.4 phần bài tập bổ sung trang 159 SBT toán 8 tập 2

    Giải bài 4.4 phần bài tập bổ sung trang 159 sách bài tập toán 8. Quan sát hình chóp tứ giác đều ở hình bs.17 rồi điền số thích hợp vào các ô trống trong bảng sau ...

  • Bài 4.5 phần bài tập bổ sung trang 159 SBT toán 8 tập 2

    Giải bài 4.5 phần bài tập bổ sung trang 159 sách bài tập toán 8. Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hai đáy ...

  • Bài 4.2 phần bài tập bổ sung trang 158 SBT toán 8 tập 2

    Giải bài 4.2 phần bài tập bổ sung trang 158 sách bài tập toán 8. Một con kiến đang ở vị trí M là trung điểm cạnh A’D’ của một chiếc hộp hình lập phương ABCD.A’B’C’D’ (h. bs.16).

  • Bài 4.1 phần bài tập bổ sung trang 158 SBT toán 8 tập 2

    Bài 4.1 phần bài tập bổ sung trang 158 SBT toán 8 tập 2. Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:

  • Bài 90 trang 157 SBT toán 8 tập 2

    Giải bài 90 trang 157 sách bài tập toán 8. Tính thể tích của một trụ bê tông cho theo các kích thước ở hình 166, SJ = 9, OI = IJ.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store