Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 71 trang 116 SBT toán 9 tập 1


Giải bài 71 trang 116 sách bài tập toán 9. Một chiếc diều ABCD có AB = BC, AD = DC...

Đề bài

Một chiếc diều \(ABCD\) có \(AB = BC, AD = DC.\) Biết \(AB = 12cm,\widehat {ADC} = 40^\circ \)

\(\widehat {ABC} = 90^\circ \) (h.25)  

  

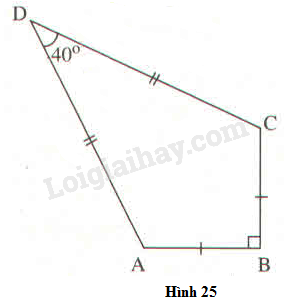
Hãy tính:

a) Chiều dài cạnh \(AD;\)

b) Diện tích của chiếc diều.

Phương pháp giải - Xem chi tiết

+ Sử dụng định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông 

+ Sử dụng quan hệ giữa cạnh và góc trong tam giác vuông: Cho tam giác \(ABC\) vuông tại \(A\) thì \(AB=BC.\sin \widehat C, \) \(BC = \dfrac{{AB}}{{\sin \widehat C}}\)

+ Diện tích diều \(S= {S_{ABC}} + {S_{ADC}}\)

Lời giải chi tiết

 

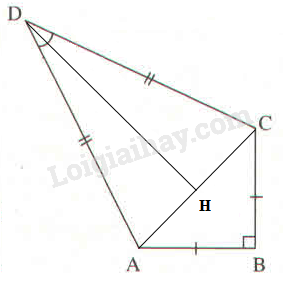
a) Nối \(AC\) và kẻ \(DH \bot AC\)

Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABC,\) ta có:

\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr 
& = {12^2} + {12^2} = 144 + 144 = 288 \cr} \)

Suy ra: \(AC = 12\sqrt 2 \,(cm)\)

Ta có: tam giác \(ACD\) cân tại \(D\) mà \(DH \bot AC\) nên DH cũng là đường trung tuyến và đường phân giác của tam giác. 

Suy ra: \(\displaystyle  HA = HC = {{AC} \over 2} = 6\sqrt 2 \,(cm)\)

Và \(\displaystyle  \widehat {ADH} = {1 \over 2}\widehat {ADC} = 20^\circ \)

Trong tam giác vuông \(ADH,\) ta có:

\(\eqalign{
& {\rm{AD = }}\displaystyle {{AH} \over {\sin \widehat {ADH}}} \cr 
& = {{6\sqrt 2 } \over {\sin 20^\circ }} \approx 24,809\,(cm) \cr} \)

b) Ta có:

\(\displaystyle  {S_{ABC}} = {1 \over 2}.AB.BC \)\(\displaystyle = {1 \over 2}.12.12 = 72\,(cm^2)\)

Trong tam giác vuông \(ADH,\) ta có:

\(\eqalign{
& DH = AH.\cot \widehat {ADH} \cr 
& = 6\sqrt 2 .\cot 20^\circ \approx 23,313\,(cm) \cr} \)

Mặt khác:

\(\eqalign{
& {S_{ADC}} = {1 \over 2}.DH.AC \cr 
& \approx {1 \over 2}.23,313.12\sqrt 2 = 197,817 cm^2 \cr} \) 

Vậy diện tích diều là:

\(\eqalign{
& S= {S_{ABC}} + {S_{ADC}} \cr 
& = 72 + 197,817 = 269,817 cm^2.\cr} \) 

Loigiaihay.com


Bình chọn:
4.4 trên 14 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store