Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 54 trang 113 SBT toán 9 tập 1


Giải bài 54 trang 113 sách bài tập toán 9. Cho hình: Biết: AB = AC = 8cm, CD = 6cm,...

Đề bài

Cho hình:

 

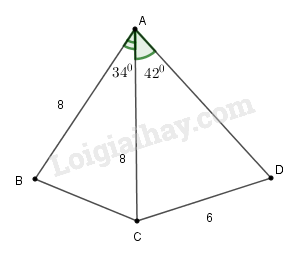
Biết:

\(AB = AC = 8cm, CD = 6cm,\) \(\widehat {BAC} = 34^\circ \) và \(\widehat {CAD} = 42^\circ .\) Tính

a) Độ dài cạnh \(BC;\) 

b) \(\widehat {ADC}\);

c) Khoảng cách từ điểm \(B\) đến cạnh \(AD.\)

Phương pháp giải - Xem chi tiết

Cho hình vẽ: 

 

 Ta có: \(AB=BC. \sin \alpha \)

Lời giải chi tiết

  

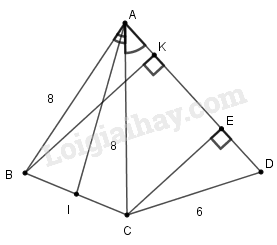
a)  Kẻ \(AI \bot BC\)

Vì \(\Delta ABC\) cân tại A nên AI vừa là đường cao, vừa là đường trung tuyến, đường phân giác nên: 

\(BI = CI = \dfrac{1}{ 2}BC\) 

và \(\widehat {BAI} = \dfrac{1}{ 2}\widehat {BAC} = \dfrac{1}{2}.34^\circ  = 17^\circ \)  

Trong tam giác vuông \(AIB\), ta có:

\(BI = AB.\sin \widehat {BAI}\)\( = 8.\sin 17^\circ  \approx 2,339\left( {cm} \right)\)

\(BC = 2.BI = 2.2,339 = 4,678\left( {cm} \right)\)

b) Kẻ \(CE \bot AD\) \(\left( {E \in AD} \right)\)

Trong tam giác vuông \(CEA\), ta có:

\(CE = AC.\sin \widehat {CAE}\)\( = 8.\sin 42^\circ  \approx 5,353\left( {cm} \right)\)

Trong tam giác vuông \(CED\), ta có:

\(\sin \widehat {ACD} = \dfrac{{CE}}{{CD}} = \dfrac{{5,353}}{6}\)\( \approx 0,8922 \Rightarrow \widehat {ADC} \approx 63^\circ 9'\)

c) Kẻ \(BK \bot AD\) \(\left( {K \in AD} \right)\)

\(\widehat {BAK} = \widehat {BAC} + \widehat {CAK} \)\(= {34^0} + {42^0} = {76^0}\)

Trong tam giác vuông \(ABK\), ta có:

\(BK = AB.\sin \widehat {BAK}\)\( = 8.\sin 76^\circ  \approx 7,762\left( {cm} \right)\)

Loigiaihay.com


Bình chọn:
4.8 trên 37 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store