Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 4.5 phần bài tập bổ sung trang 117 SBT toán 9 Tập 1


Giải bài 4.5 phần bài tập bổ sung trang 117 sách bài tập toán 9. Hãy tìm diện tích của tam giác cân có góc ở đáy bằng α nếu biết a) Cạnh bên bằng b ; b) Cạnh đáy bằng a.

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Hãy tìm diện tích của tam giác cân có góc ở đáy bằng \(α\) nếu biết:

a) Cạnh bên bằng \(b ;\)                        

b) Cạnh đáy bằng \(a.\)

Phương pháp giải - Xem chi tiết

Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác \(ABC\) vuông tại \(A\) có \(AB=c,\,AC=b,\, BC=a\) thì:   

\(b=a.sin\,B=a.cos\,C\)

\(b=c.tan\,B=c.cot\,C\)

\(c=a.sin\,C=a.cos\,B\)

\(c=b.tan\,C=b.cot\,B\)

Lời giải chi tiết

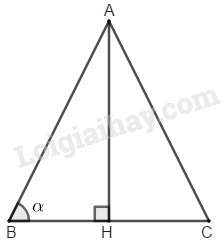
Xét tam giác cân \(ABC\) có \(AB = AC,\) \(\widehat {ABC} = \alpha, \) đường cao \(AH\)

a) \(AB = AC = b\)

Xét tam giác ABH vuông tại H ta có:

\(AH =AB.\sinα= b.\sinα,\) \( BH =AB.\cos α= b.cosα\) nên diện tích tam giác \(ABC\) là 

\(\eqalign{
& S = {1 \over 2}AH.BC = AH.BH \cr 
& = {b^2}\sin \alpha \cos \alpha . \cr} \)

b) \(BC = a\) 

Vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến. Suy ra \(BH = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Xét tam giác ABH vuông tại H, ta có: \(AH =BH.\tan \alpha = \eqalign{a \over 2}tan\alpha \)

nên diện tích tam giác \(ABC\) là: \(S = \eqalign{1 \over 2}.BC.AH\)\(=\dfrac{a}{2}.\dfrac{a}{2}\tan \alpha  = \eqalign{{{a^2}} \over 4}tan\alpha \).

Loigiaihay.com


Bình chọn:
4.1 trên 11 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua