Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 4.8 phần bài tâp bổ sung trang 117 SBT toán 9 Tập 1


Giải bài 4.8 phần bài tâp bổ sung trang 117 sách bài tập toán 9. Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đó kẻ từ M. Chứng minh rằng:...

Đề bài

Cho tam giác nhọn \(MNP.\) Gọi \(D\) là chân đường cao của tam giác đó kẻ từ \(M.\) Chứng minh rằng:

a) \({S_{MNP}} = \dfrac{1}{2}MP.NP.\sin P;\)

b) \(DP = \dfrac{MN.sinN}{tan P};\)

c) \(∆DNE\) \(\backsim\) \(∆MNP,\) trong đó \(E\) là chân đường cao của tam giác \(MNP\) kẻ từ \(P.\)

Phương pháp giải - Xem chi tiết

Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác \(ABC\) vuông tại \(A\) có \(AB=c,\,AC=b,\, BC=a\) thì:   

\(b=a.sin\,B=a.cos\,C\)

\(b=c.tan\,B=c.cot\,C\)

\(c=a.sin\,C=a.cos\,B\)

\(c=b.tan\,C=b.cot\,B\)

Xét các trường hợp hai tam giác đồng dạng.

Lời giải chi tiết

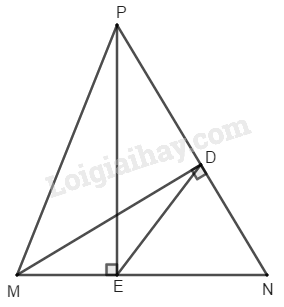
a) Xét tam giác MDP vuông tại D, ta có: \(MD = MP.sin\, P,\) suy ra: 

\({S_{MNP}} = \dfrac{1}{2}NP.MD \) \(= \dfrac{1}{2}NP.MP\sin P.\)

b) Xét tam giác MDN vuông tại D, ta có: \(MD = MN.sin \,N\)

Xét tam giác MDP vuông tại D, ta có: \(MD = DP.tan \,P\)

Suy ra \(DP=\dfrac{{MD}}{{\tan P}}=\dfrac{MN.sin N}{tan P}\)

c) Xét \(\Delta DMN\) và \(\Delta EPN\) có:

\(\widehat D = \widehat E\,( = 9{0^0})\)

\(\widehat N\) chung

Vậy \(\Delta DMN\) \(\backsim\) \(\Delta EPN\) (g-g)

\( \Rightarrow \dfrac{{DN}}{{MN}} = \dfrac{{EN}}{{PN}}\)

Xét \(\Delta DNE\) và \(\Delta MNP\) có:

\(\widehat N\) chung

\(\dfrac{{DN}}{{MN}} = \dfrac{{EN}}{{PN}}\)

Vậy \(\Delta DNE\) \(\backsim\) \(\Delta MNP\) (c-g-c).

Loigiaihay.com


Bình chọn:
4.2 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store