Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 65 trang 115 SBT toán 9 Tập 1


Giải bài 65 trang 115 sách bài tập toán 9. Tính diện tích hình thang cân, biết hai cạnh đáy là 12cm và 18cm, góc ở đáy bằng 75 độ.

Đề bài

Tính diện tích hình thang cân, biết hai cạnh đáy là \(12\,cm\) và \(18\,cm,\) góc ở đáy bằng \(75\)\(^\circ \)

Phương pháp giải - Xem chi tiết

Áp dụng công thức tính diện tích hình thang: \(S=\dfrac{a+b}{2}.h\)

Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác \(ABC\) vuông tại \(A\) có \(AB=c,\,AC=b,\, BC=a\) thì:   

\(b=a.sin\,B=a.cos\,C\)

\(b=c.tan\,B=c.cot\,C\)

\(c=a.sin\,C=a.cos\,B\)

\(c=b.tan\,C=b.cot\,B\)

Lời giải chi tiết

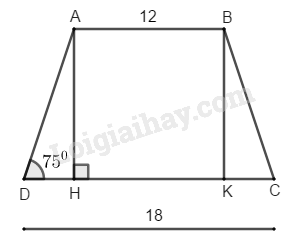
Giả sử hình thang cân \(ABCD\) có \(AB = 12\,cm,\, CD = 18\,cm,\) \(\widehat D = 75^\circ \)

Kẻ \(AH \bot CD,BK \bot CD\) suy ra \(AH//BK\) 

Lại có \(AB//HK\) nên ABKH là hình bình hành. 

Suy ra: \(AB = HK = 12\, (cm)\)

Vì \(ABCD\) là hình thang cân nên \(\widehat D = \widehat C,AD=BC\)

Nên \(\Delta ADH = \Delta BCK\) (cạnh huyền, góc nhọn)

Suy ra: \(DH = CK\) (2 cạnh tương ứng)

Suy ra: 

\(CK=DH = \dfrac{CD - HK} {2} = \dfrac{18 - 12}{2} \) \(= 3\,(cm)\)

Trong tam giác vuông \(ADH,\) ta có:

\(AH = DH.tgD = 3.tg75^\circ \) \(\approx 11,196\,(cm)\)

Vậy:

\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr 
& \approx {{12 + 18} \over 2}.11,196 = 167,94 cm^2.\cr} \) 


Bình chọn:
4.7 trên 23 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store