Lớp 12
-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ÔN TẬP VẢ BỔ TÚC VỀ SỐ TỰ NHIÊN
- Bài 1. Tập hợp. Phần tử của tập hợp
- Bài 2. Tập hợp các số tự nhiên
- Bài 3. Ghi số tự nhiên
- Bài 4. Số phần tử của một tập hợp. Tập hợp con
- Bài 5. Phép cộng và phép nhân
- Bài 6. Phép trừ và phép chia
- Bài 7. Luỹ thừa với số mũ tự nhiên, nhân hai luỹ thừa cùng cơ số
- Bài 8. Chia hai luỹ thừa cũng cơ số
- Bài 9. Thứ tự thực hiện các phép tính
- Bài 10. Tính chất chia hết của một tổng
- Bài 11. Dấu hiệu chia hết cho 2, cho 5
- Bài 12. Dấu hiệu chia hết cho 3, cho 9
- Bài 13. Ước và bội
- Bài 14. Số nguyên tố, hợp số. Bảng nguyên tố
- Bài 15. Phân tích một số ra thừa số nguyên tố
- Bài 16. Ước chung và bội chung
- Bài 17. Ước chung lớn nhất
- Bài 18. Bội chung nhỏ nhất
- Ôn tập chương 1 - Ôn tập và bổ túc về số tự nhiên
-
CHƯƠNG 2: SỐ NGUYÊN
- Bài 1. Làm quen với số nguyên âm
- Bài 2. Tập hợp các số nguyên
- Bài 3. Thứ tự trong tập hợp các số nguyên
- Bài 4. Cộng hai số nguyên cùng dấu
- Bài 5. Cộng hai số nguyên khác dấu
- Bài 6. Tính chất của phép cộng các số nguyên
- Bài 7. Phép trừ hai số nguyên
- Bài 8. Quy tắc dấu ngoặc
- Bài 9. Quy tắc chuyển vế
- Bài 10. Nhân hai số nguyên khác dấu
- Bài 11. Nhân hai số nguyên cùng dấu
- Bài 12. Tính chất của phép nhân
- Bài 13. Bội và ước của một số nguyên
- Ôn tập chương 2 - Số nguyên
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ĐOẠN THẲNG
- Bài 1. Điểm. Đường thẳng
- Bài 2. Ba điểm thẳng hàng
- Bài 3. Đường thẳng đi qua hai điểm
- Bài 4. Thực hành trồng cây thẳng hàng
- Bài 5. Tia
- Bài 6. Đoạn thẳng
- Bài 7. Độ dài đoạn thẳng
- Bài 8. Khi nào thì AM + MB = AB?
- Bài 9. Vẽ đoạn thẳng cho biết độ dài
- Bài 10. Trung điểm của đoạn thẳng
- Ôn tập chương 1 - Đoạn thẳng
-
-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 2
-
CHƯƠNG 3: PHÂN SỐ
- Bài 1. Mở rộng khái niệm phân số
- Bài 2. Phân số bằng nhau
- Bài 3. Tính chất cơ bản của phân số
- Bài 4. Rút gọn phân số
- Bài 5. Quy đồng mẫu nhiều phân số
- Bài 6. So sánh phân số
- Bài 7. Phép cộng phân số
- Bài 8. Tính chất cơ bản của phép cộng phân số
- Bài 9. Phép trừ phân số
- Bài 10. Phép nhân phân số
- Bài 11. Tính chất cơ bản của phép nhân phân số
- Bài 12. Phép chia phân số
- Bài 13. Hỗn số. Số thập phân. Phần trăm
- Bài 14. Tìm giá trị phân số của một số cho trước
- Bài 15. Tìm một số biết giá trị một phân số của nó
- Bài 16. Tìm tỉ số của hai số
- Bài 17. Biểu đồ phần trăm
- Bài tập ôn tập chương 3 - Phân số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 2
Bài 64 trang 137 SBT toán 6 tập 1
Giải bài 64 trang 137 sách bài tập toán 6. Cho đoạn thẳng AB và trung điểm M của nó. Chứng tỏ rằng nếu C là điểm nằm giữa M và B...
Đề bài
Cho đoạn thẳng \(AB\) và trung điểm \(M\) của nó. Chứng tỏ rằng nếu \(C\) là điểm nằm giữa \(M \) và \(B\) thì \(\displaystyle CM = {{CA - CB} \over 2}\)
Phương pháp giải - Xem chi tiết
+ Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì \(AM + MB = AB.\)
+ Trung điểm \(M\) của đoạn thẳng \(AB\) là điểm nằm giữa \(A, B\) và cách đều \(A, B \,(MA = MB).\)
Lời giải chi tiết
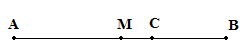
Vì \(M\) là trung điểm \(AB\) nên \(AM = BM\)
Vì \(M\) nằm giữa \(A\) và \(C\) nên \(AM + MC = AC\)
Vì \(C \) nằm giữa \(B\) và \(M\) nên \(BC + MC = BM \) \(\Rightarrow BC = BM – MC\)
Suy ra: \(AC > BC\)
Ta có: \(AC – BC \) \(= (AM + MC) – (BM – MC)\) \(= AM + MC – BM + MC\) \(= 2MC\)
\(\displaystyle \Rightarrow CM = {{CA - CB} \over 2}\)
Loigiaihay.com
Sub đăng ký kênh giúp Ad nhé !
Bình luận
Các bài liên quan: - Bài 10. Trung điểm của đoạn thẳng
>> Học trực tuyến lớp 6 trên Tuyensinh247.com mọi lúc, mọi nơi với đầy đủ các môn: Toán, Văn, Anh, Lý, Sử, Sinh, Địa cùng các thầy cô nổi tiếng, dạy hay dễ hiểu
 |
 |
 |
 |
 |
 |
 |
Gửi bài
