Bài 3.1, 3.2, 3.3, 3.4 phần bài tập bổ sung trang 41 SBT toán 6 tập 2

Bài III.1

Phân số \(\displaystyle {a \over b}\) sau khi rút gọn được phân số \(\displaystyle {{ - 8} \over {11}}\). Biết \(b\, – a = 190\). Tìm phân số \(\displaystyle {a \over b}\).

Phương pháp giải:

Từ đề bài ra có \(\displaystyle {a \over b} = {{ - 8} \over {11}}\), lấy \(1\) trừ lần lượt vào hai vế của đẳng thức ta thu được:  \(\displaystyle {{b - a} \over b} = {{11 + 8} \over {11}}\)        \((1)\)

Thay \(b\; – a = 190\) vào \((1)\) ta tìm được \(b\), từ đó tìm được \(a = b- 190.\)

Lời giải chi tiết:

\(\displaystyle {a \over b} = {{ - 8} \over {11}}\) suy ra \(\displaystyle 1 - {a \over b} = 1 - {{ - 8} \over {11}}\) hay \(\displaystyle {{b } \over b}-{{ a} \over b} = {{11 + 8} \over {11}}\) 

Suy ra \(\displaystyle {{b-a} \over b} = {{19} \over {11}}\)      \((1)\)

Thay \(b\; – a = 190\) vào \((1)\) ta được: \(\displaystyle {{190} \over b} = {{19} \over {11}} \Rightarrow 19.b = 190.11\)\( \Rightarrow b = 190.11:19 \Rightarrow b = 110\)

Lại có \(a=b-190\) \(\Rightarrow a  = 110 - 190 = 110 - 190 =-80.\)

Phân số \(\displaystyle {a \over b}\) phải tìm là \(\displaystyle {{ - 80} \over {110}}\).

Bài III.2

Tính \(\displaystyle A = \left( {{{878787} \over {959595}} + {{ - 8787} \over {9595}}} \right).{{1234321} \over {5678765}}\)

Phương pháp giải:

- Rút gọn phân số \(\displaystyle \dfrac {878787}{959595}\) bằng cách chia cả tử và mẫu cho \(10101.\)

- Rút gọn phân số \(\displaystyle \dfrac{ - 8787}{9595}\) bằng cách chia cả tử và mẫu cho \(10101.\)

Lời giải chi tiết:

Ta có :

\(\displaystyle {{878787} \over {959595}} = {{878787:10101} \over {959595:10101}} = {{87} \over {95}}\)

\(\displaystyle {{8787} \over {9595}} = {{8787:101} \over {9595:101}} = {{87} \over {95}}\)

\(\displaystyle A = \left( {{{878787} \over {959595}} + {{ - 8787} \over {9595}}} \right).{{1234321} \over {5678765}}\)

\(\Rightarrow\)\(\displaystyle A = \left( {{{87} \over {95}} + {{ - 87} \over {95}}} \right).{{1234321} \over {5678765}}\)

\(\Rightarrow\)\(\displaystyle A = 0.{{1234321} \over {5678765}} = 0.\)

Bài III.3

Cho \(\displaystyle A = {{2009.2010 - 2} \over {2008 + 2008.2010}};\) \(\displaystyle B = {{ - 2009.20102010} \over {20092009.2010}}\)

Tính \(A + B.\)

Phương pháp giải:

- Biến đổi tử số của phân số \(A\) thành \(\left( {2008 + 1} \right).2010 - 2\)\(= 2008.2010 + 2010 - 2 \)\(=2008 + 2008.2010\), từ đó ra rút gọn được phân số \(A\).

- Rút gọn phân số \(B\) bằng cách tách tử số và mẫu số thành tích của các thừa số, sau đó chia cả tử và mẫu cho các thừa số chung.

Lời giải chi tiết:

\(\displaystyle A = {{2009.2010 - 2} \over {2008 + 2008.2010}} \)\(\displaystyle= {{\left( {2008 + 1} \right).2010 - 2} \over {2008 + 2008.2010}}\)

\(\displaystyle = {{2008.2010 + 2010 - 2} \over {2008 + 2008.2010}} \)\(\displaystyle = {{2008.2010 + 2008} \over {2008 + 2008.2010}} = 1\)

\(\displaystyle B =  = {{ - 2009.20102010} \over {20092009.2010}} \)\(\displaystyle= {{ - 2009.2010.10001} \over {2009.10001.2010}} =  - 1\)

Do đó : \(A + B = 1 + (-1) = 0.\)

Bài III.4

Tính giá trị của biểu thức :

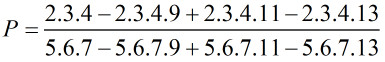
Phương pháp giải:

Áp dụng công thức nhân một số với một tổng hoặc một hiệu:

\(a . b + a .c = a. (b+c)\) 

\(a .b - a.c = a. (b-c)\) 

Lời giải chi tiết:

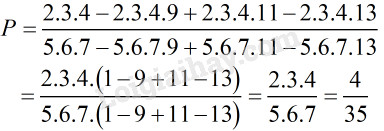
Loigiaihay.com