-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 24 trang 83 SBT toán 8 tập 1
Giải bài 24 trang 83 sách bài tập toán 8. Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN...
Đề bài
Cho tam giác \(ABC\) cân tại \(A.\) Trên các cạnh bên \(AB,\) \(AC\) lấy các điểm \(M,\) \(N\) sao cho \(BM = CN.\)
\(a)\) Tứ giác \(BMNC\) là hình gì \(?\) Vì sao \(?\)
\(b)\) Tính các góc của tứ giác \(BMNC\) biết rằng \(\widehat A = {40^0}\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết
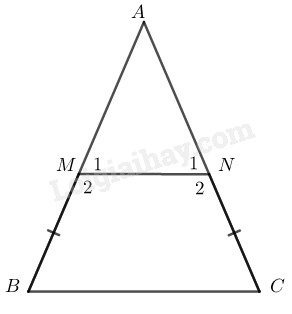
\(a)\) \(∆ ABC\) cân tại \(A\)
\( \Rightarrow \widehat B = \widehat C \) (tính chất tam giác cân)
Mà \( \widehat B + \widehat C +\widehat A=180^0 \) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat B + \widehat C =180^0-\widehat A\)
\( \Rightarrow 2\widehat B =180^0-\widehat A\)
\( \Rightarrow \widehat B = \widehat C= \displaystyle {{{{180}^0} - \widehat A} \over 2}\) \((1)\)
\(AB = AC\;\;\; (gt) \)
\(⇒ AM + BM= AN+ CN\)
mà \(BM = CN \;\;\; (gt)\)
suy ra: \(AM = AN\)
\(⇒ ∆ AMN\) cân tại \(A\)
\( \Rightarrow {\widehat M_1} = {\widehat N_1} \) ( tính chất tam giác cân)
Mà \({\widehat M_1} + {\widehat N_1}+\widehat A=180^0 \) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat M_1 + \widehat N_1 =180^0-\widehat A\)
\( \Rightarrow 2\widehat M_1 =180^0-\widehat A\)
\( \Rightarrow {\widehat M_1} = {\widehat N_1}= \displaystyle {{{{180}^0} - \widehat A} \over 2}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \({\widehat M_1} = \widehat B\)
\(⇒MN // BC\) ( vì có các cặp góc đồng vị bằng nhau)
Tứ giác \(BCMN\) là hình thang có \(\widehat B = \widehat C\). Vậy \(BCMN\) là hình thang cân.
\(b)\) Với \(\widehat A = {40^0}\) thì \(\widehat B = \widehat C =\displaystyle {{{{180}^0} - \widehat A} \over 2}\)\( = \displaystyle {{{{180}^0} - {{40}^0}} \over 2} = {70^0}\)
Vì \(MN//BC\) nên \({\widehat M_2} + \widehat B = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow {\widehat M_2} = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}\)
Vì \(BCMN\) là hình thang cân nên \({\widehat N_2} = {\widehat M_2} = {110^0}\) (tính chất hình thang cân)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 25 trang 83 SBT toán 8 tập 1
- Bài 26 trang 83 SBT toán 8 tập 1
- Bài 27 trang 83 SBT toán 8 tập 1
- Bài 28 trang 83 SBT toán 8 tập 1
- Bài 29 trang 83 SBT toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
