Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Hình học 9
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Hình học 9
Đề bài
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A. Một tiếp tuyến chung ngoài BC của (O) và (O’) (\(B ∈ (O), C ∈ (O’)\)).
a. Chứng minh rằng đường tròn đường kính BC tiếp xúc với đường thẳng OO’ và đường tròn đường kính OO’ tiếp xúc với đường thẳng BC.
b. Tính BC theo R và R’
c. Đường tròn (H; r) tiếp xúc với cả hai đường tròn (O), (O’) và tiếp xúc với BC tại M. Tính bán kính r theo R và R’.
LG ý a
Phương pháp giải:
Sử dụng:
-Tính chất hai tiếp tuyến cắt nhau
-Đường trung bình của hình thang
- Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính là tiếp tuyến của đường tròn đó
Lời giải chi tiết:
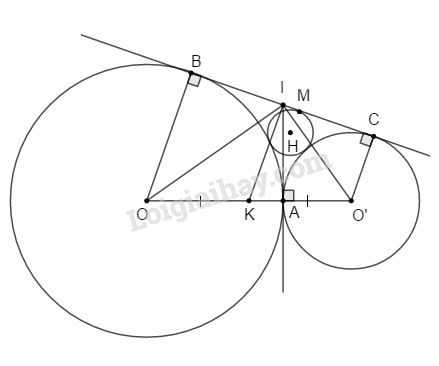
a. Gọi I là giao điểm của tiếp tuyến tại A và tiếp tuyến chung BC, ta có \(IA = IB = IC\) (tính chất tiếp tuyến cắt nhau).
Ta có: O, A, O’ thẳng hàng nên \(IA ⊥ OO’\)
Chứng tỏ đường tròn tâm I đường kính BC tiếp xúc với đường thẳng OO’.
Gọi K là trung điểm của OO’ \(⇒\) IK là đường trung bình của hình thang BOO’C \(⇒\) IK // OB // O’C hay \(IK ⊥ BC.\)
Mặt khác : \(IK = {{OB + O'C} \over 2} = {{R + R'} \over 2} = {{OO'} \over 2}\)\( \Rightarrow IK = OK = O'K\)
Suy ra BC là tiếp tuyến của đường tròn tâm K đường kính OO'
Do đó đường tròn tâm K đường kính OO’, tiếp xúc với BC tại I.
LG ý b
Phương pháp giải:
Sử dụng:
-Hai tia phân giác của hai góc kề bù tạo thành 1 góc vuông
-Hệ thức về cạnh và đường cao trong tam giác vuông
Lời giải chi tiết:
b. Ta có: OI, O’I theo thứ tự là phân giác của các góc BIA và CIA nên \(OI ⊥ O’I\) hay ∆OIO’ vuông tại I có đường cao IA.
\(I{A^2} = OA.O'A = R.R'\) (định lí 2) hay \(IA = \sqrt {R.R'} \Rightarrow BC = 2\sqrt {R.R'} \)
LG ý c
Phương pháp giải:
Sử dụng kết quả của ý b
Lời giải chi tiết:
c. Ta có: BM là tiếp tuyến chung ngoài của (O) và (H) nên:
\(BM = 2\sqrt {R.r} \) (chứng minh như câu b)
Tương tự ta có : \(CM = 2\sqrt {R'.r} ,\) mà \(BC = BM + MC\)
\(\eqalign{ & \Rightarrow 2\sqrt {R.R'} = 2\sqrt {R.r} + 2\sqrt {R'.r} \cr& \Rightarrow \sqrt {R.R'} = \sqrt r \left( {\sqrt R + \sqrt {R'} } \right) \cr & \Rightarrow \sqrt r = {{\sqrt {R.R'} } \over {\sqrt R + \sqrt {R'} }} \cr&\Rightarrow r = {{R.R'} \over {R + R' + 2\sqrt {R.R'} }} \cr} \)
Loigiaihay.com
- Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 8 - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 9 - Chương 2 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận