Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Sự xác định của đường tròn. Tính chất đối xứng c..

Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 2 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 2 - Hình học 9

Đề bài

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, R, S lần lượt là trung điểm của các cạnh AB, BC, CD và DA. 

a. Chứng minh rằng bốn điểm M, N, R, S thuộc cùng một đường tròn.

b. Cho \(AC = 24cm, BD = 18cm.\) Tính bán kính đường tròn ngoại tiếp tứ giác MNRS.

Phương pháp giải - Xem chi tiết

Sử dụng:

a) Để chứng minh 4 điểm cùng thuộc một đường tròn, ta chứng minh 4 điểm đó cùng cách đều một điểm cố định.

Chỉ ra tứ giác MNRS là hình chữ nhật rồi sử dụng tính chất: Hai đường chéo của hình chữ nhật bằng nhau và giao nhau tại trung điểm mỗi đường

b) Định lý Pytago: Cho tam giác \(ABC\) vuông tại \(A\), ta có: \(B{C^2} = A{B^2} + A{C^2}\)

Lời giải chi tiết

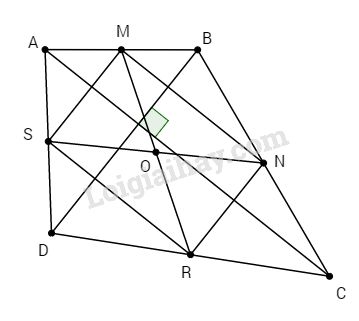
a. Ta có: M, N lần lượt là trung điểm của AB và BC (gt) nên MN là đường trung bình của ∆ABC.

Do đó : MN // AC (1)

Tương tự SR là đường trung bình của ∆ADC nên SR // AC  (2)

Từ (1) và (2) ⇒ MN // RS // AC (3)

Chứng minh tương tự ta có: MS // NR // BD  (4)

Từ (3) và (4) ⇒ MNRS là hình bình hành (các cạnh đối song song)

Mặt khác AC ⊥ BD (gt) ⇒ MN ⊥ MS nên hình bình hành MNRS là hình chữ nhật.

Gọi O là giao điểm của hai đường chéo MR và NS ta có:

OM = ON = OR = OS

Chứng tỏ bốn điểm M, N, R, S thuộc cùng một đường tròn tâm O.

b. Ta có: MN là đường trung bình của ∆ABC (cmt), ta có:

\(MN = {1 \over 2}AC = {1 \over 2}.24 = 12\,\left( {cm} \right)\)

Tương tự: \(MS = {1 \over 2}BD = 9\,\left( {cm} \right)\)

Lại có ∆MNS vuông tại M (cmt) ta có:

\(SN = \sqrt {M{N^2} + M{S^2}}  \)\(\;= \sqrt {{{\left( {12} \right)}^2} + {{\left( 9 \right)}^2}}  = 15\left( {cm} \right)\)

Vậy đường tròn ngoại tiếp tứ giác MNRS có tâm O và bán kính là

\({{SN} \over 2} = {{15} \over 2} = 7,5\,\left( {cm} \right)\)

Loigiaihay.com


Bình chọn:
2.7 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store