-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 1
-
CHƯƠNG I. CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng Căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương I – Căn bậc hai. Căn bậc ba
- Đề kiểm tra 15 phút - Chương I - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương I - Đại số 9
-
CHƯƠNG II. HÀM SỐ BẬC NHẤT
- Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số
- Bài 2. Hàm số bậc nhất
- Bài 3. Đồ thị của hàm số y = ax + b (a ≠ 0)
- Bài 4. Đường thẳng song song và đường thẳng cắt nhau
- Bài 5. Hệ số góc của đường thẳng y = ax + b (a ≠ 0).
- Ôn tập chương II – Hàm số bậc nhất
- Đề kiểm tra 15 phút - Chương 2 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 1
-
CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
- Đề kiểm tra 15 phút - Chương 1 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Hình học 9
-
CHƯƠNG II. ĐƯỜNG TRÒN
- Bài 1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương II – Đường tròn
- Đề kiểm tra 15 phút - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 9
-
-
Đề cương ôn tập học kì 1
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 2
-
CHƯƠNG III. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
- Bài 1. Phương trình bậc nhất hai ẩn
- Bài 2. Hệ hai phương trình bậc nhất hai ẩn
- Bài 3. Giải hệ phương trình bằng phương pháp thế
- Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số.
- Bài 5. Giải bài toán bằng cách lập hệ phương trình
- Bài 6. Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
- Ôn tập Chương III Hệ hai phương trình bậc nhất hai ẩn
- Đề kiểm 15 phút - Chương 3 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số 9
-
CHƯƠNG IV. HÀM SỐ y = ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương IV - Hàm số y = ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
- Đề kiểm tra 15 phút - Chương 4 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 2
-
CHƯƠNG III. GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Ôn tập chương III – Góc với đường tròn
- Đề kiểm tra 15 phút - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 9
-
CHƯƠNG IV. HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Hình học 9
-
BÀI TẬP ÔN CUỐI NĂM - TOÁN 9
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 9
-
Tải 30 đề kiểm tra giữa kì 1 Toán 9
-
Tải 30 đề ôn tập học kì 1 Toán 9
-
Tải 30 đề thi học kì 1 của các trường Toán 9
-
Tải 30 đề kiểm tra giữa kì 2 Toán 9
-
Tải 30 đề ôn tập học kì 2 Toán 9
-
Tải 30 đề thi học kì 2 của các trường Toán 9
Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 4 - Đại số 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 4 - Đại số 9
Đề bài
Bài 1: Cho hàm số \(y = f\left( x \right) = {x^2}.\)
a) Vẽ đồ thị của hàm số.
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số khi x thỏa mãn \(0 \le x \le 2.\)
Bài 2: Tìm giá trị của m, biết rằng hàm số \(y = \left( {1 - m} \right){x^2}\) đồng biến khi \(x > 0.\)
Bài 3: Cho hàm số \(y = \left( {m - 1} \right){x^2}\). Tìm giá trị của m biết đồ thị (P) của hàm số đi qua điểm \(A(2; − 4).\)
LG bài 1
Phương pháp giải:
a.Các bước vẽ đồ thị:
+Tìm tập xác định của hàm số.
+Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
+Vẽ đồ thị và kết luận.
b. Chứng minh hàm số đồng biến và sử dụng:
\(a \le x \le b \Leftrightarrow f\left( a \right) \le f\left( x \right) \le f\left( b \right)\)
Lời giải chi tiết:
Bài 1: a) Bảng giá trị :
|
x |
− 2 |
− 1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Đồ thị của hàm số là một parabol có đỉnh là O và nhận trục Oy làm trục đối xứng.
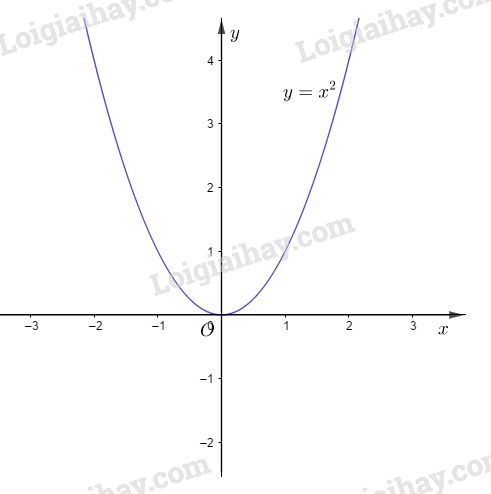
b) Ta có \(a = 1 > 0\) nên hàm số đồng biến khi \(x > 0.\)
Vậy \(0 \le x \le 2 \Rightarrow f\left( 0 \right) \le f\left( x \right) \le f\left( 2 \right)\)\(\; \Rightarrow 0 \le {x^2} \le 4.\)
Vậy giá trị nhỏ nhất của hàm số bằng 0, khi \(x = 0\); giá trị lớn nhất của hàm số bằng 4, khi \(x = 2.\)
LG bài 2
Phương pháp giải:
Do x>0 nên hàm số đồng biến khi a>0
Lời giải chi tiết:
Bài 2: Hàm số đồng biến khi \(x > 0 \Leftrightarrow 1 – m > 0 \Leftrightarrow m < 1.\)
LG bài 3
Phương pháp giải:
Thế tọa độ của A vào hàm số ta tìm được m
Lời giải chi tiết:
Bài 3: Ta có \(A \in (P) \Rightarrow - 4 = \left( {m - 1} \right){.2^2} \)
\(\;\Rightarrow m - 1 = - 1 \Rightarrow m = 0.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 4 - Đại số 9
- Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 4 - Đại số 9
- Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 4 - Đại số 9
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 4 - Đại số 9
- Bài 3 trang 31 SGK Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
