Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 4 : Chu vi và diện tích hình tròn

Bài 20 trang 112 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Từ điểm A trên nửa đường tròn (O) đường kính BC, vẽ ra ngài tam giác ABC hai nửa đường tròn

Đề bài

Từ điểm A trên nửa đường tròn (O) đường kính BC, vẽ ra ngài tam giác ABC hai nửa đường tròn đường kính AB và AC (AB<AC, xem hình vẽ). Chứng minh rằng: diện tích S của tam giác ABC bằng tổng hai diện tích S1 và S2 của hai hình trăng khuyết là phần của hai nửa đường tròn đường kính AB và AC ở ngoài nửa đường tròn đường kính BC.

 

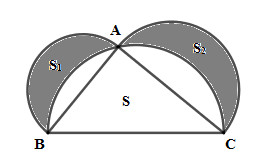
Phương pháp giải - Xem chi tiết

Sử dụng công thức tính diện tích hình tròn và định lí Pytago.

Lời giải chi tiết

 

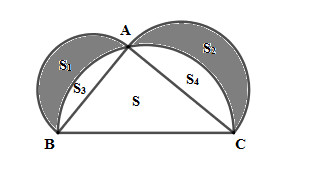
Diện tích nửa hình tròn đường kính AB là \(\pi {\left( {\dfrac{{AB}}{2}} \right)^2} = {S_1} + {S_3} \)

\(\Rightarrow {S_1} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} - {S_3}\)

Diện tích nửa hình tròn đường kính AC là \(\pi {\left( {\dfrac{{AC}}{2}} \right)^2} = {S_2} + {S_4} \)

\(\Rightarrow {S_3} = \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - {S_4}\)

\(\begin{array}{l} \Rightarrow {S_1} + {S_2} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} - {S_3} + \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - {S_4} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} + \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right)\\ \Rightarrow {S_1} + {S_2} = \dfrac{\pi }{4}\left( {A{B^2} + A{C^2}} \right) - \left( {{S_3} + {S_4}} \right)\end{array}\)

Diện tích nửa hình tròn đường kính BC là \(\pi {\left( {\dfrac{{BC}}{2}} \right)^2} = {S_3} + {S_4} + S \Rightarrow S = \pi {\left( {\dfrac{{BC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right)\)

Vì \(\widehat {BAC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại A.

Áp dụng định lí Pytago ta có: \(B{C^2} = A{B^2} + A{C^2}\)

\( \Rightarrow {S_1} + {S_2} = \dfrac{\pi }{4}.B{C^2} - \left( {{S_3} + {S_4}} \right) = \dfrac{\pi }{4}{\left( {\dfrac{{BC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right) = S\).

Vậy \(S = {S_1} + {S_2}\).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store