Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 4 : Chu vi và diện tích hình tròn

Bài 7 trang 111 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Trên đường tròn (O; R) lần lượt lấy ba điểm A, B, C theo thứ tự sao cho

Đề bài

Trên đường tròn (O; R) lần lượt lấy ba điểm A, B, C theo thứ tự sao cho \(AB = R\sqrt 2 \) và sđ cung BC=300.

a) Tính số đo của cung AB không chứa điểm C và tính độ dài dây AC theo R.

b) Từ A vẽ đường thẳng vuông góc với đường thẳng BC tại D. Tính độ dài các cung AD, DB, AB của đường tròn (ABD) theo R.

Phương pháp giải - Xem chi tiết

a) Chứng minh tam giác OAB vuông tại O suy ra số đo cung AB.

Gọi H là trung điểm của AC, chứng minh H là trung điểm của AC, tính AH, từ đó suy ra AC.

b) Xác định tâm đường tròn ngoại tiếp tam giác ABD, tính số đo các góc \(\widehat {AO'D};\,\,\widehat {BO'D};\,\,\widehat {AO'B}\) với O’ là tâm đường tròn ngoại tiếp tam giác ABD.

Sử dụng công thức tính độ dài cung n0 của đường tròn có bán kính R là \(l = \dfrac{{\pi Rn}}{{180}}\).

Lời giải chi tiết

 

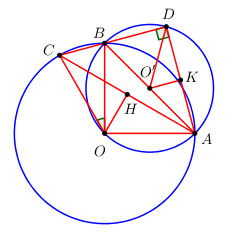
a) Xét tam giác OAB có : \(O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2} = A{B^2}\)

\( \Rightarrow \Delta OAB\) vuông tại O (định lí Pytago đảo)

\( \Rightarrow \widehat {AOB} = {90^0} = sdcung\,AB\) (số đo góc ở tâm bằng số đo cung bị chắn).

Mà \(sdcung\,BC = {30^0} \Rightarrow \widehat {BOC} = {30^0}\)(số đo góc ở tâm bằng số đo cung bị chắn).

\( \Rightarrow \widehat {AOC} = \widehat {AOB} + \widehat {BOC} = {90^0} + {30^0} = {120^0}\).

Gọi H là trung điểm của AC ta có \(OH \bot AC\) (quan hệ vuông góc giữa đường kính và dây cung).

Xét tam giác OAC có \(OA = OC = R \Rightarrow \Delta OAC\) cân tại O \( \Rightarrow OH\) là đường cao đồng thời là phân giác \( \Rightarrow \widehat {AOH} = \dfrac{1}{2}\widehat {AOC} = \dfrac{1}{2}{.120^0} = {60^0}\).

Xét tam giác vuông OAH có : \(AH = OA.\sin {60^0} = R.\dfrac{{\sqrt 3 }}{2}\)

\( \Rightarrow AC = 2AH = 2.R.\dfrac{{\sqrt 3 }}{2} = R\sqrt 3 \).

b) Tam giác ABD vuông tại D nên nội tiếp đường tròn đường kính AB, bán kính \(r = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 2 }}{2}\)

Xét tam giác OBC có \(OB = OC = R \Rightarrow \Delta OBC\) cân tại O

\( \Rightarrow \widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^0}\)

Ta có : \(\widehat {OBD} + \widehat {OBC} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {OBD} = {180^0} - \widehat {OBC} = {180^0} - {75^0} = {105^0}\)

Tứ giác OADB có \(\widehat {AOB} + \widehat {ADB} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OADB là tứ giác nội tiếp

\( \Rightarrow \widehat {OAD} + \widehat {OBD} = {180^0}\) (tổng 2 góc đối của tứ giác nội tiếp)

\( \Rightarrow \widehat {OAD} = {180^0} - \widehat {OBD} = {180^0} - {105^0} = {75^0}\).

Mà \(\widehat {OAB} + \widehat {BAD} = \widehat {AOD} \)

\(\Rightarrow {45^0} + \widehat {BAD} = {75^0} \Rightarrow \widehat {BAD} = {30^0}\)

(do \(\Delta OAB\) vuông cân tại O nên \(\widehat {OAB} = \widehat {OBA} = {45^0}\))

Gọi O’ là trung điểm của AB.

Tam giác O’AD có \(O'A = O'D \Rightarrow \Delta O'AD\) cân tại O’

\( \Rightarrow \widehat {AO'D} = {180^0} - \widehat {O'AD} - \widehat {O'DA} \)\(\,= {180^0} - 2\widehat {O'AD} = {180^0} - {2.30^0} = {120^0}\)

\( \Rightarrow {l_{AD}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi .\dfrac{{R\sqrt 2 }}{2}.120}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{3}\)

Ta có \(\widehat {BO'D} + \widehat {AO'D} = {180^0}\) (kề bù) \( \Rightarrow \widehat {BO'D} = {180^0} - \widehat {AO'D} = {180^0} - {120^0} = {60^0}\)

\( \Rightarrow {l_{DB}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi .\dfrac{{R\sqrt 2 }}{2}.60}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{6}\)

\({l_{AB}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi \dfrac{{R\sqrt 2 }}{2}180}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{2}\)

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store