Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 4 : Chu vi và diện tích hình tròn

Bài 6 trang 111 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Cho cung AB trên đường tròn (O; R)

Đề bài

Cho cung AB trên đường tròn (O; R)

a) Tính \(\widehat {AOB}\) khi biết có độ dài \(l = \dfrac{{\pi R}}{4}\) .

b) Chọn điểm C trên đường tròn sao cho AC cắt đoạn OB và OAC là tam giác đều. Tính độ dài các cung lớn AC và  BC.

Phương pháp giải - Xem chi tiết

Sử dụng các công thức \(l = \dfrac{{\pi Rn}}{{180}}\).

Lời giải chi tiết

 

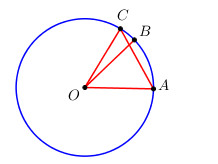
a) Ta có \(l = \dfrac{{\pi R}}{4} \Leftrightarrow \dfrac{{\pi Rn}}{{180}} = \dfrac{{\pi R}}{4}\)

\(\Leftrightarrow \dfrac{n}{{180}} = \dfrac{1}{4} \Leftrightarrow n = {45^0}\).

Vì \(\widehat {AOB}\) là góc ở tâm \( \Rightarrow \widehat {AOB} = sdcung\,AB = {45^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).

b) Ta có \(sdcung\,AC = \widehat {AOC} = {60^0}\)

Khi đó độ dài cung lớn AC là độ dài của cung \({360^0} - {60^0} = {300^0} \Rightarrow \)độ dài cung lớn AC bằng \(\dfrac{{\pi R.300}}{{180}} = \dfrac{{5\pi R}}{3}\).

Ta có: \(cung\,AB + cung\,BC = cung\,AC\) \( \Rightarrow {45^0} + cung\,BC = {60^0}\)

\(\Leftrightarrow cung\,BC = {15^0}\).

Khi đó độ dài cung lớn BC là độ dài của cung \({360^0} - {15^0} = {345^0} \)

\(\Rightarrow \) độ dài cung lớn BC bằng \(\dfrac{{\pi R.345}}{{180}} = \dfrac{{23\pi R}}{{12}}\).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store