-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 4 : Chu vi và diện tích hình tròn
Bài 9 trang 111 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho hai đường tròn đồng tâm có khoảng cách ngắn nhất giữa hai điểm thuộc hai đường tròn
Đề bài
Cho hai đường tròn đồng tâm có khoảng cách ngắn nhất giữa hai điểm thuộc hai đường tròn bằng 1m. Tính hiệu các chu vi của hai đường tròn.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính chu vi đường tròn bán kính R là \(2\pi R\).
Lời giải chi tiết
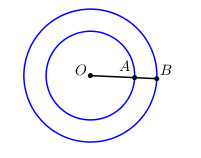
Lấy điểm A, B lần lượt thuộc 2 đường tròn sao cho O, A, B thẳng hàng.
Vì khoảng cách ngắn nhất giữa hai điểm thuộc hai đường tròn bằng 1m nên \(AB = 1m\).
Đặt \(OA = R \Rightarrow OB = OA + AB = R + 1\).
Chu vi đường tròn tâm O, bán kính OA là \({C_1} = 2\pi OA = 2\pi R\).
Chu vi đường tròn tâm O, bán kính OB là \({C_2} = 2\pi OB = 2\pi \left( {R + 1} \right) = 2\pi R + 2\pi \).
Vậy hiệu các chu vi của 2 đường tròn là \({C_2} - {C_1} = 2\pi R + 2\pi - 2\pi R = 2\pi \).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 111 Tài liệu dạy – học Toán 9 tập 2
- Bài 11 trang 112 Tài liệu dạy – học Toán 9 tập 2
- Bài 12 trang 112 Tài liệu dạy – học Toán 9 tập 2
- Bài 13 trang 112 Tài liệu dạy – học Toán 9 tập 2
- Bài 14 trang 112 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
