Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 7 : Đường thẳng và đường tròn.

Bài 16 trang 146 Tài liệu dạy – học Toán 9 tập 1


Giải bài tập Cho hai đường tròn (O) và (O’) cắt nhau tại A và B.

Đề bài

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ cát tuyến chung MAN sao cho MA=AN. Đường vuông góc với MN tại A cắt OO’ tại I. Chứng minh I là trung điểm của OO’.

Phương pháp giải - Xem chi tiết

+) Gọi H và K lần lượt là trung điểm của \(AM\) và \(AN\), chứng minh  A là trung điểm của HK và \(OHKO'\) là hình thang.

+) Sử dụng tính chất đường trung bình của hình thang.

Lời giải chi tiết

 

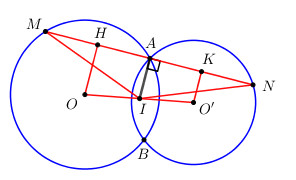
Gọi H và K lần lượt là trung điểm của \(AM\) và \(AN\) ta có: \(AH = \dfrac{1}{2}AM,\,\,AK = \dfrac{1}{2}AN \)

\(\Rightarrow AH = AK\) \( \Rightarrow \) A là trung điểm của \(HK\).

Áp dụng quan hệ vuông góc giữa đường kính và dây cung ta có: \(\left\{ \begin{array}{l}OH \bot AM\\O'K \bot AN\end{array} \right. \Rightarrow OH\parallel O'K \Rightarrow \) Tứ giác \(OHKO'\) là hình thang.

Xét hình thang  \(OHKO'\) ta có:

\(A\) là trung điểm của \(HK\).

\(IA \bot MN \Rightarrow IA//OH//O'K\)

Do đó \(I\) là trung điểm của \(OO'\) (đpcm).

 Loigiaihay.com


Bình chọn:
4 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store