Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 7 : Đường thẳng và đường tròn.

Bài 15 trang 146 Tài liệu dạy – học Toán 9 tập 1


Giải bài tập Cho hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại A và B

Đề bài

Cho hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại A và B với R > R’. Vẽ các đường kính AOC và AO’D. Chứng minh rằng ba điểm B, C, D thẳng hàng.

Phương pháp giải - Xem chi tiết

Sử dụng định lí đường trung tuyến trong tam giác vuông chứng minh \(\angle ABC = \angle ABD = {90^0}\).

Lời giải chi tiết

 

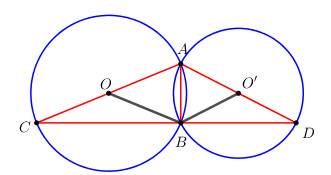
Xét tam giác \(ABC\) ta có \(OB = OA = OC = \dfrac{1}{2}AB \)

\(\Rightarrow \Delta ABC\) vuông tại B (Tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy) \( \Rightarrow \angle ABC = {90^0}\).

Hoàn toàn tương tự ta chứng minh được \(\Delta ABD\) vuông tại \(B \Rightarrow \angle ABD = {90^0}\).

Do đó \(\angle CBD = \angle ABC + \angle ABD\) \(\; = {90^0} + {90^0} = {180^0}\).

Vậy \(B,\,\,C,\,\,D\) thẳng hàng.

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store